【题目】已知数列{an}的前n项和为Tn= ![]() n2﹣
n2﹣ ![]() n,且an+2+3log4bn=0(n∈N*)
n,且an+2+3log4bn=0(n∈N*)
(1)求{bn}的通项公式;
(2)数列{cn}满足cn=anbn , 求数列{cn}的前n项和Sn;
(3)若cn≤ ![]() m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
参考答案:
【答案】
(1)解:由Tn= ![]() n2﹣
n2﹣ ![]() n,易得an=3n﹣2代入到an+2+3log4bn=0(n∈N*)根据对数的运算性质化简bn=
n,易得an=3n﹣2代入到an+2+3log4bn=0(n∈N*)根据对数的运算性质化简bn= ![]() (n∈N*),
(n∈N*),
(2)解:cn=anbn= ![]() ,∴
,∴ ![]() ∴
∴ ![]()
两式相减整理得 ![]()
(3)解:cn=anbn=(3n﹣2) ![]() ∴cn+1﹣cn=(3n+1)
∴cn+1﹣cn=(3n+1) ![]() ﹣(3n﹣2)
﹣(3n﹣2) ![]() =9(1﹣n)
=9(1﹣n) ![]() (n∈N*),
(n∈N*),
∴当n=1时,c2=c1= ![]() ,
,
当n≥2时,cn+1<cn,即c1=c2>c3>…>cn,
∴当n=1时,cn取最大值是 ![]() ,又cn≤
,又cn≤ ![]() m2+m﹣1对一切正整数n恒成立∴
m2+m﹣1对一切正整数n恒成立∴ ![]() m2+m﹣1≥
m2+m﹣1≥ ![]() ,即m2+4m﹣5≥0,
,即m2+4m﹣5≥0,
解得:m≥1或m≤﹣5.
【解析】(1)由Tn= ![]() n2﹣
n2﹣ ![]() n,先求数列{an}的通项公式;代入到an+2+3log4bn=0(n∈N*)根据对数的运算性质化简即可求出{bn}的通项公式;(2)把第一问求出的两数列的通项公式代入cn=anbn中,确定出cn的通项公式,从而求数列{cn}的前n项和Sn;(3)表示出cn+1﹣cn , 判断得到其差小于0,故数列{cn}为递减数列,令n=1求出数列{cn}的最大值,然后原不等式的右边大于等于求出的最大值,列出关于m的一元二次不等式,求出不等式的解集即为实数m的取值范围.
n,先求数列{an}的通项公式;代入到an+2+3log4bn=0(n∈N*)根据对数的运算性质化简即可求出{bn}的通项公式;(2)把第一问求出的两数列的通项公式代入cn=anbn中,确定出cn的通项公式,从而求数列{cn}的前n项和Sn;(3)表示出cn+1﹣cn , 判断得到其差小于0,故数列{cn}为递减数列,令n=1求出数列{cn}的最大值,然后原不等式的右边大于等于求出的最大值,列出关于m的一元二次不等式,求出不等式的解集即为实数m的取值范围.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系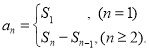 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方体ABCD﹣A′B′C′D′.
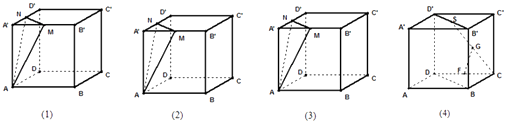
(1)设M,N分别是A′D′,A′B′的中点,试在下列三个正方体中各作出一个过正方体顶点且与平面AMN平行的平面(不用写过程)
(2)设S是B′D′的中点,F,G分别是DC,SC的中点,求证:直线GF∥平面BDD′B′. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中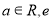 为自然对数的底数.
为自然对数的底数.(1)函数
 的图象能否与
的图象能否与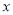 轴相切?若能与
轴相切?若能与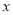 轴相切,求实数
轴相切,求实数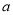 的值;否则,请说明理由;
的值;否则,请说明理由;(2)若函数
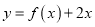 在
在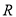 上单调递增,求实数
上单调递增,求实数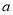 能取到的最大整数值.
能取到的最大整数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,动圆
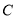 与圆
与圆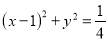 外切,且与直线
外切,且与直线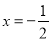 相切,记圆心
相切,记圆心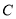 的轨迹为曲线
的轨迹为曲线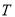 .
.(1)求曲线
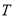 的方程;
的方程;(2)设过定点
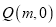 (
(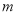 为非零常数)的动直线
为非零常数)的动直线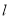 与曲线
与曲线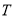 交于
交于 两点,问:在曲线
两点,问:在曲线 上是否存在点
上是否存在点 (与
(与 两点相异),当直线
两点相异),当直线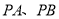 的斜率存在时,直线
的斜率存在时,直线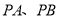 的斜率之和为定值.若存在,求出点
的斜率之和为定值.若存在,求出点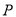 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=ax2+bx+c.
(1)若f(﹣1)=0,试判断函数f(x)零点个数;
(2)若对x1x2∈R,且x1<x2 , f(x1)≠f(x2),证明方程f(x)=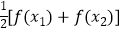 必有一个实数根属于(x1 , x2).
必有一个实数根属于(x1 , x2).
(3)是否存在a,b,c∈R,使f(x)同时满足以下条件
①当x=﹣1时,函数f(x)有最小值0;
②对任意x∈R,都有0≤f(x)﹣x≤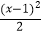 若存在,求出a,b,c的值,若不存在,请说明理由.
若存在,求出a,b,c的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在极坐标系中,点
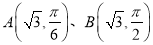 ,曲线
,曲线 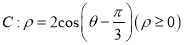 ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为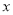 轴正半轴建立直角坐标系.
轴正半轴建立直角坐标系.(1)在直角坐标系中,求点
 的直角坐标及曲线
的直角坐标及曲线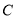 的参数方程;
的参数方程;(2)设点
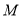 为曲线
为曲线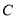 上的动点,求
上的动点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
 中,
中,  为
为 的中点,
的中点,  ,
,  .
.
(1)求证:
 平面
平面 ;
;(2)当
 时,求直线
时,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
相关试题

