搜索
【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，S表示△ABC的面积，若acosB+bcosA=csinC，S= 
（b2+c2﹣a2），则∠B=（ ）
A.90°
B.60°
C.45°
D.30°
参考答案：
【答案】C
【解析】解：由正弦定理可知acosB+bcosA=2RsinAcosB+2RsinBcosA=2Rsin（A+B）=2RsinC=2RsinCsinC∴sinC=1，C= 
．
∴S= 
ab= 
（b2+c2﹣a2），
解得a=b，因此∠B=45°．
故选C
先利用正弦定理把题设等式中的边转化成角的正弦，化简整理求得sinC的值，进而求得C，然后利用三角形面积公式求得S的表达式，进而求得a=b，推断出三角形为等腰直角三角形，进而求得∠B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知数列{an}：
， 
+ 
， 
+ 
+ 
， 
+ 
+ 
+ 
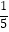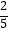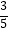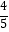，…，那么数列{bn}={ 
}的前n项和为（ ）
A.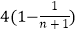
B.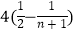
C.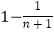
D.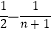
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数f（x）=ax2+bx+c和一次函数g（x）=﹣bx，其中a，b，c∈R且满足a＞b＞c，f（1）=0．
（1）证明：函数f（x）与g（x）的图象交于不同的两点；
（2）若函数F（x）=f（x）﹣g（x）在[2，3]上的最小值为9，最大值为21，试求a，b的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=|x﹣1|+|x﹣a|．
（1）若a=2，解不等式f（x）≥2；
（2）已知f（x）是偶函数，求a的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】定义在R上的奇函数f（x），当x＞0时，f（x）=x﹣2
（1）求函数f（x）的解析式；
（2）求不等式f（x）＜2的解集． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=x﹣alnx，（a∈R）．
（1）讨论函数f（x）在定义域内的极值点的个数；
（2）设g（x）=﹣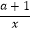
，若不等式f（x）＞g（x）对任意x∈[1，e]恒成立，求a的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知y=
x3+bx2+（b+2）x+3是R上的单调增函数，则b的取值是（ ）
A.b＜﹣1或b＞2
B.b≤﹣2或b≥2
C.﹣1＜b＜2
D.﹣1≤b≤2
相关试题
