【题目】2014年3月的“两会”上,李克强总理在政府工作报告中,首次提出“倡导全民阅读”,某学校响应政府倡导,在学生中发起读书热潮.现统计了从2014年下半年以来,学生每半年人均读书量,如下表:
时间 | 2014年下半年 | 2015年上半年 | 2015年下半年 | 2016年上半年 | 2016年下半年 |
时间代号 |
|
|
|
|
|
人均读书量 |
|
|
|
|
|
根据散点图,可以判断出人均读书量![]() 与时间代号
与时间代号![]() 具有线性相关关系.
具有线性相关关系.
(1)求![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(2)根据所求的回归方程,预测该校2017年上半年的人均读书量.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
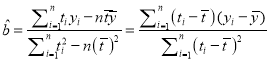 ,
, ![]()
参考答案:
【答案】(1) ![]() .(2)
.(2) ![]() 本.
本.
【解析】试题分析:(1) 先算出![]() ,再由
,再由 ,算出
,算出![]() ,从而可得
,从而可得![]() 的值,进而可得回归方程;(2) )将2017年上半年的时间代号
的值,进而可得回归方程;(2) )将2017年上半年的时间代号![]() 代入(1)的回归方程可得结果.
代入(1)的回归方程可得结果.
试题解析:(1)由已知表格的数据,得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 关于
关于![]() 的线性回归方程是
的线性回归方程是![]() .
.
(2)将2017年上半年的时间代号![]() 代入(1)的回归方程,得
代入(1)的回归方程,得![]() ,故预测该校2017年上半年的学生人均读书量约为
,故预测该校2017年上半年的学生人均读书量约为![]() 本.
本.
【方法点晴】本题主要考查线性回归方程求法与应用,属于中档题.求回归直线方程的步骤:①依据样本数据画出散点图,确定两个变量具有线性相关关系;②计算![]() 的值;③计算回归系数
的值;③计算回归系数![]() ;④写出回归直线方程为
;④写出回归直线方程为![]() ;(2) 回归直线过样本点中心
;(2) 回归直线过样本点中心![]() 是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
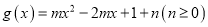 在
在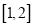 上有最大值1和最小值0,设
上有最大值1和最小值0,设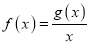 .
.(1)求
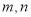 的值;
的值;(2)若不等式
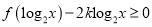 在
在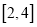 上有解,求实数
上有解,求实数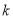 的取值范围;
的取值范围;(3)若方程
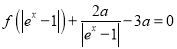 (
(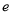 为自然对数的底数)有三个不同的实数解,求实数
为自然对数的底数)有三个不同的实数解,求实数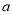 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
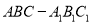 中,底面
中,底面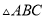 是边长为2的等边三角形,
是边长为2的等边三角形, 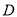 为
为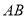 的中点.
的中点.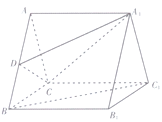
(1)求证:
 平面
平面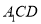 ;
;(2)若四边形
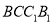 是正方形,且
是正方形,且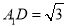 ,求直线
,求直线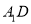 与平面
与平面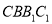 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
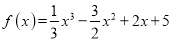 .
.(Ⅰ)求
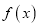 的单调区间;
的单调区间;(Ⅱ)若曲线
 与
与 有三个不同的交点,求实数
有三个不同的交点,求实数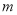 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场进行有奖促销活动,顾客购物每满500元,可选择返回50元现金或参加一次抽奖,抽奖规则如下:从1个装有6个白球、4个红球的箱子中任摸一球,摸到红球就可获得100元现金奖励,假设顾客抽奖的结果相互独立.
(Ⅰ)若顾客选择参加一次抽奖,求他获得100元现金奖励的概率;
(Ⅱ)某顾客已购物1500元,作为商场经理,是希望顾客直接选择返回150元现金,还是选择参加3次抽奖?说明理由;
(Ⅲ)若顾客参加10次抽奖,则最有可能获得多少现金奖励?
-
科目: 来源: 题型:
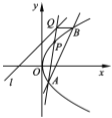
查看答案和解析>>【题目】已知直线
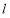 的方程为
的方程为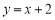 ,点
,点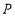 是抛物线
是抛物线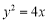 上到直线
上到直线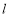 距离最小的点,点
距离最小的点,点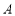 是抛物线上异于点
是抛物线上异于点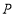 的点,直线
的点,直线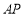 与直线
与直线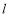 交于点
交于点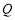 ,过点
,过点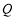 与
与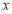 轴平行的直线与抛物线
轴平行的直线与抛物线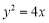 交于点
交于点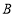 .
.
(Ⅰ)求点
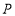 的坐标;
的坐标;(Ⅱ)证明直线
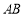 恒过定点,并求这个定点的坐标.
恒过定点,并求这个定点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 ,
,  ,函数
,函数 的图象过点
的图象过点 ,点
,点 与其相邻的最高点的距离为
与其相邻的最高点的距离为 .
.(1)求
 的单调递增区间;
的单调递增区间;(2)计算
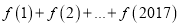 ;
;(3)设函数
 ,试讨论函数
,试讨论函数 在区间
在区间 上的零点个数.
上的零点个数.
相关试题

