【题目】已知f(x)=2x2﹣3x+1,g(x)=ksin(x﹣ ![]() )(k≠0).
)(k≠0).
(1)设f(x)的定义域为[0,3],值域为A; g(x)的定义域为[0,3],值域为B,且AB,求实数k的取值范围.
(2)若方程f(sinx)+sinx﹣a=0在[0,2π)上恰有两个解,求实数a的取值范围.
参考答案:
【答案】
(1)解:当x∈[0,3]时,由于f(x)=2x2﹣3x+1图象的对称轴为 ![]() ,且开口向上,
,且开口向上,
可知 ![]() ,f(x)max=f(3)=10,
,f(x)max=f(3)=10,
所以f(x)的值域 ![]() ;
;
当x∈[0,3]时, ![]() ,
, ![]() ;所以当k>0时,g(x)的值域
;所以当k>0时,g(x)的值域 ![]() ;
;
所以当k<0时,g(x)的值域 ![]() ;
;
又∵AB,所以 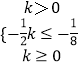 或
或 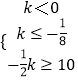 ;
;
即 k≥10或k≤﹣20;
(2)解:∵f(sinx)+sinx﹣a=0,所以2sin2x﹣2sinx+1﹣a=0在x∈[0,2π)上恰有两个解,…
设t=sinx,则t∈[﹣1,1],令h(t)=2t2﹣2t+1﹣a,
①当t∈(﹣1,1)时,由题意h(t)=0恰有一个解或者有两个相等的解,
即h(﹣1)h(﹣1)<0或△=4﹣8(1﹣a)=0,即1<a<5或 ![]()
②若t=﹣1是方程2t2﹣2t+1﹣a=0的一个根,此时a=5,且方程的另一个根为t=2,于是sinx=﹣1或sinx=2,
因此 ![]() ,不符合题意,故a=5(舍);
,不符合题意,故a=5(舍);
③若t=1是方程2t2﹣2t+1﹣a=0的一个根,此时a=1,且方程的另一个根为t=0,于是sinx=1或sinx=0,
因此x=0或 ![]() 或π,不符合题意,故a=1(舍);
或π,不符合题意,故a=1(舍);
综上,a的取值范围是1<a<5或 ![]() .
.
【解析】(1)根据二次函数和正弦函数的图象与性质,分别求出f(x)、g(x)在区间[0,3]上的最值即得值域A、B;再根据AB求出k的取值范围;(2)根据f(sinx)+sinx﹣a=0在x∈[0,2π)上恰有两个解,利用换元法设t=sinx,t∈[﹣1,1],构造函数h(t)=2t2﹣2t+1﹣a,讨论t的取值范围,从而求出实数a的取值范围.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(
 x+φ),x∈R,A>0,0<φ<
x+φ),x∈R,A>0,0<φ<  .y=f(x)的部分图象如图所示,P、Q 分别为该图象的最高点和最低点,点P的坐标为(1,A).点R的坐标为(1,0),∠PRQ=
.y=f(x)的部分图象如图所示,P、Q 分别为该图象的最高点和最低点,点P的坐标为(1,A).点R的坐标为(1,0),∠PRQ= 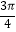 .
. 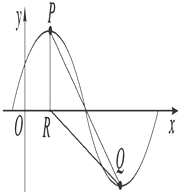
(1)求f(x)的最小正周期以及解析式.
(2)用五点法画出f(x)在x∈[﹣ ,
, 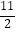 ]上的图象.
]上的图象. -
科目: 来源: 题型:
查看答案和解析>>【题目】某单位职工义务献血,在体检合格的人中,
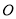 型血的共有28人,
型血的共有28人, 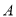 型血的共有7人,
型血的共有7人, 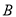 型血的共有9人,
型血的共有9人, 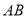 型血的有3人.
型血的有3人.(1)从中任选1人去献血,有多少种不同的选法?
(2)从四种血型的人中各选1人去献血,有多少种不同的选法?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
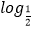 [
[ 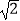 sin(x﹣
sin(x﹣  )].
)].
(1)求f(x)的定义域和值域;
(2)说明f(x)的奇偶性;
(3)求f(x)的单调增区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】有4位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学上、下午各测试一个项目,且不重复.若上午不测“握力”项目,下午不测“台阶”项目,其余项目上、下午都各测试一人,则不同的安排方式共有__________种(用数字作答).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
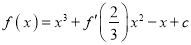 ,(其中
,(其中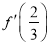 为
为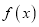 在点
在点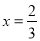 处的导数,
处的导数, 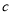 为常数).
为常数).(1)求
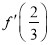 的值;
的值;(2)求函数
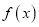 的单调区间;
的单调区间;(3)设函数
 ,若函数
,若函数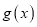 在区间
在区间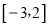 上单调递增,求实数
上单调递增,求实数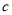 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的中心在原点,离心率等于
的中心在原点,离心率等于 ,它的一个短轴端点恰好是抛物线
,它的一个短轴端点恰好是抛物线 的焦点
的焦点(1)求椭圆
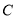 的方程;
的方程;(2)已知
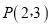 、
、 是椭圆上的两点,
是椭圆上的两点,  ,
, 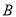 是椭圆上位于直线
是椭圆上位于直线 两侧的动点.①若直线
两侧的动点.①若直线 的斜率为
的斜率为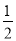 ,求四边形
,求四边形 面积的最大值;
面积的最大值;②当
 ,
,  运动时,满足
运动时,满足 ,试问直线
,试问直线 的斜率是否为定值,请说明理由
的斜率是否为定值,请说明理由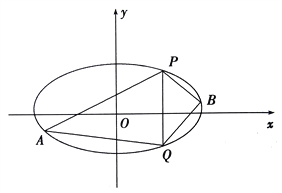
相关试题

