【题目】已知函数f(x)=Asin( ![]() x+φ),x∈R,A>0,0<φ<
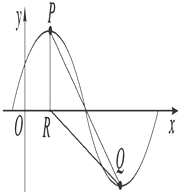
x+φ),x∈R,A>0,0<φ< ![]() .y=f(x)的部分图象如图所示,P、Q 分别为该图象的最高点和最低点,点P的坐标为(1,A).点R的坐标为(1,0),∠PRQ=
.y=f(x)的部分图象如图所示,P、Q 分别为该图象的最高点和最低点,点P的坐标为(1,A).点R的坐标为(1,0),∠PRQ= ![]() .
. 
(1)求f(x)的最小正周期以及解析式.
(2)用五点法画出f(x)在x∈[﹣ ![]() ,
, ![]() ]上的图象.
]上的图象.
参考答案:
【答案】
(1)解:由题意得:f(x)的最小正周期 ![]() ,
,
因为P(1,A)在 ![]() 的图象上,
的图象上,
所以 ![]() ,
,
所以 ![]() ,即
,即 ![]() ,
,
又因为 ![]() ,
,
因此, ![]()
过Q做QD⊥x轴,垂足为D,设D(x0,0),则Q(x0,﹣A),由周期为6可知,RD=3,
由于 ![]() ,
,
所以 ![]() ,于是QD=RD=3,
,于是QD=RD=3,
所以A=3,
∴ ![]()
(2)解:列表如下:
x | ﹣0.5 | 1 | 2.5 | 4 | 5.5 |
| 0 |
| π |
| 2π |
| 0 | 3 | 0 | ﹣3 | 0 |
描点连线,作图如下:
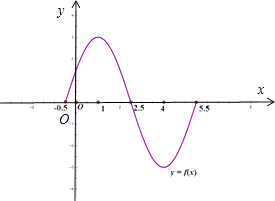
【解析】(1)根据周期公式求出函数f(x)的最小正周期,由P(1,A)在 ![]() 的图象上,结合范围0<φ<
的图象上,结合范围0<φ< ![]() ,可求φ,由图象和条件设出点Q的坐标,再过点Q做x轴的垂线,设垂足为D,根据条件和正切函数求出A,从而可得函数解析式;(2)利用五点作图法即可作图得解.
,可求φ,由图象和条件设出点Q的坐标,再过点Q做x轴的垂线,设垂足为D,根据条件和正切函数求出A,从而可得函数解析式;(2)利用五点作图法即可作图得解.
【考点精析】认真审题,首先需要了解五点法作函数y=Asin(ωx+φ)的图象(描点法及其特例—五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线)).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下:

分数段(分)
[50,70]
[70,90]
[90,110]
[110,130]
[130,150]
合计
频数
b
频率
a
0.25
(1)表中a,b的值及分数在[90,100)范围内的学生,并估计这次考试全校学生数学成绩及格率(分数在[90,150]范围为及格);
(2)从大于等于110分的学生随机选2名学生得分,求2名学生的平均得分大于等于130分的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】用1、2、3、4、5、6这六个数字可组成多少个无重复数字且不能被5整除的五位数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  的焦点在
的焦点在 轴上,椭圆
轴上,椭圆 的左顶点为
的左顶点为 ,斜率为
,斜率为 的直线交椭圆
的直线交椭圆 于
于 ,
,  两点,点
两点,点 在椭圆
在椭圆 上,
上,  ,直线
,直线 交
交 轴于点
轴于点 .
.(Ⅰ)当点
 为椭圆的上顶点,
为椭圆的上顶点,  的面积为
的面积为 时,求椭圆的离心率;
时,求椭圆的离心率;(Ⅱ)当
 ,
,  时,求
时,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某单位职工义务献血,在体检合格的人中,
 型血的共有28人,
型血的共有28人, 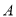 型血的共有7人,
型血的共有7人, 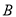 型血的共有9人,
型血的共有9人, 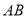 型血的有3人.
型血的有3人.(1)从中任选1人去献血,有多少种不同的选法?
(2)从四种血型的人中各选1人去献血,有多少种不同的选法?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
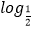 [
[ 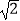 sin(x﹣
sin(x﹣  )].
)].
(1)求f(x)的定义域和值域;
(2)说明f(x)的奇偶性;
(3)求f(x)的单调增区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=2x2﹣3x+1,g(x)=ksin(x﹣
 )(k≠0).
)(k≠0).
(1)设f(x)的定义域为[0,3],值域为A; g(x)的定义域为[0,3],值域为B,且AB,求实数k的取值范围.
(2)若方程f(sinx)+sinx﹣a=0在[0,2π)上恰有两个解,求实数a的取值范围.
相关试题

