【题目】已知函数f(x)= ![]() [
[ ![]() sin(x﹣
sin(x﹣ ![]() )].
)].
(1)求f(x)的定义域和值域;
(2)说明f(x)的奇偶性;
(3)求f(x)的单调增区间.
参考答案:
【答案】
(1)解:由题意得 ![]() ,即
,即 ![]() ,
,
所以 ![]() ,
,
所以 ![]()
因此f(x)的定义域为 ![]()
又因为 ![]() ,所以
,所以 ![]() ,
,
再考察 ![]() 的图象,可知
的图象,可知 ![]() ,
,
所以f(x)的值域为 ![]()
(2)解:由(1)知f(x)的定义域不关于原点对称,故f(x)是非奇非偶函数
(3)解:由题意可知 ![]()
即 ![]() ,
,
所以f(x)的单调增区间为 ![]()
【解析】(1)根据函数成立的条件结合对数函数的性质进行求解即可.(2)根据函数奇偶性的定义进行判断(3)根据复合函数单调性之间的关系进行求解.
【考点精析】根据题目的已知条件,利用复合函数单调性的判断方法和函数的奇偶性的相关知识可以得到问题的答案,需要掌握复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”;偶函数的图象关于y轴对称;奇函数的图象关于原点对称.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  的焦点在
的焦点在 轴上,椭圆
轴上,椭圆 的左顶点为
的左顶点为 ,斜率为
,斜率为 的直线交椭圆
的直线交椭圆 于
于 ,
, 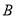 两点,点
两点,点 在椭圆
在椭圆 上,
上,  ,直线
,直线 交
交 轴于点
轴于点 .
.(Ⅰ)当点
 为椭圆的上顶点,
为椭圆的上顶点,  的面积为
的面积为 时,求椭圆的离心率;
时,求椭圆的离心率;(Ⅱ)当
 ,
,  时,求
时,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(
 x+φ),x∈R,A>0,0<φ<
x+φ),x∈R,A>0,0<φ<  .y=f(x)的部分图象如图所示,P、Q 分别为该图象的最高点和最低点,点P的坐标为(1,A).点R的坐标为(1,0),∠PRQ=
.y=f(x)的部分图象如图所示,P、Q 分别为该图象的最高点和最低点,点P的坐标为(1,A).点R的坐标为(1,0),∠PRQ= 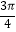 .
. 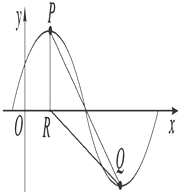
(1)求f(x)的最小正周期以及解析式.
(2)用五点法画出f(x)在x∈[﹣ ,
, 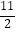 ]上的图象.
]上的图象. -
科目: 来源: 题型:
查看答案和解析>>【题目】某单位职工义务献血,在体检合格的人中,
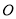 型血的共有28人,
型血的共有28人, 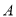 型血的共有7人,
型血的共有7人, 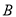 型血的共有9人,
型血的共有9人, 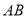 型血的有3人.
型血的有3人.(1)从中任选1人去献血,有多少种不同的选法?
(2)从四种血型的人中各选1人去献血,有多少种不同的选法?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=2x2﹣3x+1,g(x)=ksin(x﹣
 )(k≠0).
)(k≠0).
(1)设f(x)的定义域为[0,3],值域为A; g(x)的定义域为[0,3],值域为B,且AB,求实数k的取值范围.
(2)若方程f(sinx)+sinx﹣a=0在[0,2π)上恰有两个解,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】有4位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学上、下午各测试一个项目,且不重复.若上午不测“握力”项目,下午不测“台阶”项目,其余项目上、下午都各测试一人,则不同的安排方式共有__________种(用数字作答).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
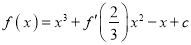 ,(其中
,(其中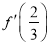 为
为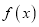 在点
在点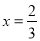 处的导数,
处的导数, 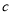 为常数).
为常数).(1)求
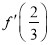 的值;
的值;(2)求函数
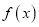 的单调区间;
的单调区间;(3)设函数
 ,若函数
,若函数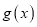 在区间
在区间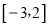 上单调递增,求实数
上单调递增,求实数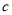 的取值范围。
的取值范围。
相关试题

