【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.
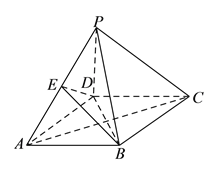
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 的交点记为
的交点记为![]() ,求证
,求证![]() 平面
平面![]() ;
;
(3)在(2)的条件下求三棱锥![]() 的体积.
的体积.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)根据等腰三角形的性质可得![]() ,根据菱形的性质可得
,根据菱形的性质可得![]() ,由线面垂直的判定定理可得
,由线面垂直的判定定理可得![]() 面
面![]() ,根据面面垂直的判定定理可得结果;(2)由
,根据面面垂直的判定定理可得结果;(2)由![]() ,
,![]() 为
为![]() 中点,可得
中点,可得![]() ,由(1)知
,由(1)知![]() ,利用线面垂直的判定定理可得结论;(3)先证明
,利用线面垂直的判定定理可得结论;(3)先证明![]() 面
面![]() ,则
,则![]() ,利用棱锥的体积公式可得结果.
,利用棱锥的体积公式可得结果.
试题解析:(1)设![]() ,连结
,连结![]() ,
,
∴![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]() ,
,
又∵底面![]() 为菱形,
为菱形,
∴![]() ,
,
∵![]() ,
,
∴![]() 面
面![]() ,
,
又∵![]() 面
面![]() ,
,
∴面![]() 面
面![]() .
.
(2)∵![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() 面
面![]() .
.
(3)过![]() 作
作![]() 于
于![]() ,
,
∴![]() ,
,
又∵![]() 面
面![]() ,
,
![]() 面
面![]() ,
,
∴![]()
![]()
![]()
![]() .
.
【方法点晴】本题主要考线面垂直的判定定理、面面垂直的判定定理以及利用等积变换求棱锥体积,属于难题.解答空间几何体中垂直关系时,一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化,转化时要正确运用有关的定理,找出足够的条件进行推理;证明直线和平面垂直的常用方法有:(1)利用判定定理;(2)利用判定定理的推论![]() ;(3)利用面面平行的性质
;(3)利用面面平行的性质![]() ;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.
;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
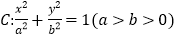 经过点
经过点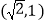 ,且离心率为
,且离心率为 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)设
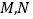 是椭圆上的点,直线
是椭圆上的点,直线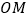 与
与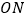 (
(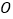 为坐标原点)的斜率之积为
为坐标原点)的斜率之积为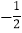 .若动点
.若动点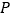 满足
满足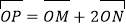 ,试探究是否存在两个定点
,试探究是否存在两个定点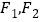 ,使得
,使得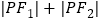 为定值?若存在,求
为定值?若存在,求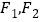 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在正三棱柱
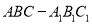 中,
中, 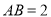 ,
, 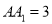 ,点
,点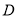 为
为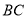 的中点.
的中点.(I)求证:
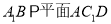 ;
;(II)若点
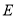 为
为 上的点,且满足
上的点,且满足 ,若二面角
,若二面角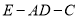 的余弦值为
的余弦值为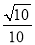 ,求实数
,求实数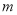 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“累积净化量
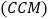 ”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据
”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据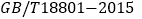 《空气净化器》国家标准,对空气净化器的累计净化量
《空气净化器》国家标准,对空气净化器的累计净化量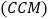 有如下等级划分:
有如下等级划分:累积净化量(克)
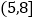
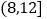
12以上
等级
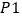
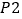
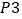
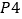
为了了解一批空气净化器(共5000台)的质量,随机抽取
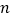 台机器作为样本进行估计,已知这
台机器作为样本进行估计,已知这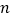 台机器的累积净化量都分布在区间
台机器的累积净化量都分布在区间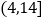 中,按照
中,按照 、
、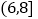 、
、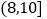 、
、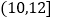 、
、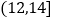 均匀分组,其中累积净化量在
均匀分组,其中累积净化量在 的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示: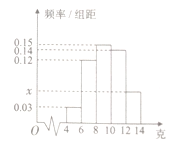
(1)求
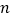 的值及频率分布直方图中
的值及频率分布直方图中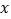 的值;
的值;(2)以样本估计总体,试估计这批空气净化器(共5000台)中等级为
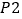 的空气净化器有多少台?
的空气净化器有多少台?(3)从累积净化量在
 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为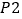 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
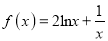 .
.(1)讨论函数
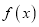 的单调性;
的单调性;(2)如果对所有的
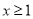 ,都有
,都有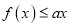 ,求
,求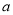 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2sin
 cos
cos  ﹣2
﹣2 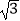 sin2
sin2  +
+ 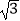
(1)求函数f(x)的单调减区间
(2)已知α∈( ,
, 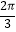 ),且f(α)=
),且f(α)= 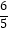 ,求f(
,求f( 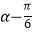 )的值.
)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
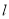 的参数方程是
的参数方程是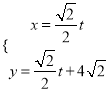 (
(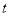 是参数),以坐标原点为原点,
是参数),以坐标原点为原点, 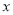 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线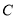 的极坐标方程为
的极坐标方程为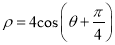 .
.(1)判断直线
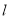 与曲线
与曲线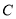 的位置关系;
的位置关系;(2)过直线
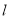 上的点作曲线
上的点作曲线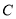 的切线,求切线长的最小值.
的切线,求切线长的最小值.
相关试题

