【题目】已知椭圆![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 是椭圆上的点,直线
是椭圆上的点,直线![]() 与
与![]() (
(![]() 为坐标原点)的斜率之积为
为坐标原点)的斜率之积为![]() .若动点
.若动点![]() 满足
满足![]() ,试探究是否存在两个定点
,试探究是否存在两个定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(Ⅰ)![]() ; (Ⅱ)见解析.
; (Ⅱ)见解析.
【解析】试题分析:(Ⅰ)利用椭圆的离心率计算公式和点在椭圆上列方程组求解即可得出.
(Ⅱ)利用向量的坐标运算、点在椭圆上满足椭圆的方程、斜率计算公式及其椭圆的定义即可得出.
试题解析:
(Ⅰ)∵![]() ∴
∴![]()
又∵椭圆![]() 经过点
经过点![]() ∴
∴![]()
解得:![]() ,
,![]()
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,
,![]() ,则由
,则由![]() 得
得
即![]() ,
,![]() ,
,
因为点![]() 在椭圆
在椭圆![]() 上,
上,
所以![]() ,
,![]()
故![]()
![]()
![]()
![]()
![]()
设![]() ,
,![]() 分别为直线
分别为直线![]() 与
与![]() 的斜率,由题意知,
的斜率,由题意知,
![]() ,因此
,因此![]()
所以![]() ,
,
所以点![]() 是椭圆
是椭圆![]() 上的点,
上的点,
所以由椭圆的定义知存在点![]() ,满足
,满足![]() 为定值
为定值
又因为![]() ,
,
所以![]() 坐标分别为
坐标分别为![]() 、
、![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一数集的任一元素的倒数仍在该集合中,则称该数集为“可倒数集”.
(1)判断集合A={-1,1,2}是否为可倒数集;
(2)试写出一个含3个元素的可倒数集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关心的话题,为了解公众对“延迟退休”的态度,某校课外研究性学习小组在某社区随机抽取了50人进行调查,将调查情况进行整理后制成下表:
年龄
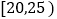
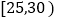
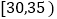
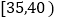
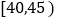
人数
4
5
8
5
3
年龄
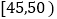
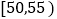
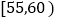
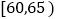
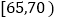
人数
6
7
3
5
4
经调查年龄在
 ,
,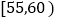 的被调查者中赞成“延迟退休”的人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
的被调查者中赞成“延迟退休”的人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.(Ⅰ)求年龄在
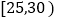 的被调查者中选取的2人都赞成“延迟退休”的概率;
的被调查者中选取的2人都赞成“延迟退休”的概率;(Ⅱ)若选中的4人中,不赞成“延迟退休”的人数为
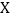 ,求随机变量
,求随机变量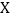 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于定义在
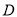 上的函数
上的函数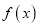 ,若存在距离为
,若存在距离为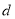 的两条直线
的两条直线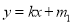 和
和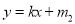 ,使得对任意
,使得对任意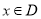 都有
都有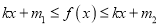 恒成立,则称函数
恒成立,则称函数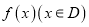 有一个宽度为
有一个宽度为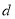 的通道,给出下列函数:①
的通道,给出下列函数:①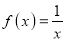 ;②
;②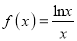 ;③
;③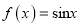 ;④
;④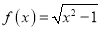 .其中在区间
.其中在区间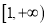 上通道宽度可以为1的函数的个数是( )
上通道宽度可以为1的函数的个数是( )A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】设A={x|x2-2x=0},B={x|x2-2ax+a2-a=0}.
(1)若A∩B=B,求a的取值范围;
(2)若A∪B=B,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
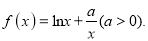
(1)若函数
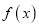 有零点,求实数
有零点,求实数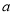 的取值范围;
的取值范围;(2)证明:当
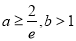 时,
时, 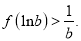
-
科目: 来源: 题型:
查看答案和解析>>【题目】某渔场有一边长为20m的正三角形湖面ABC(如图所示),计划筑一条笔直的堤坝DE将水面分成面积相等的两部分,以便进行两类水产品养殖试验(D在AB上,E在AC上).

(1)为了节约开支,堤坝应尽可能短,请问该如何设计?堤坝最短为多少?
(2)将DE设计为景观路线,堤坝应尽可能长,请问又该如何设计?
相关试题

