【题目】在正三棱柱![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(I)求证: ![]() ;
;
(II)若点![]() 为
为![]() 上的点,且满足
上的点,且满足![]() ,若二面角
,若二面角![]() 的余弦值为
的余弦值为![]() ,求实数
,求实数![]() 的值.
的值.
参考答案:
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】试题分析:(Ⅰ)连接![]() 交
交![]() 于
于![]() ,则
,则![]() 为
为![]() 的中点连接
的中点连接![]() ,则
,则![]() ,由此能证明
,由此能证明![]() 平面
平面![]() .
.
(Ⅱ)过![]() 作
作![]()
![]()
![]() 于
于![]() ,则
,则![]()
![]() 平面
平面![]() ,过
,过![]() 作
作![]()
![]()
![]() ,垂足为
,垂足为![]() ,连
,连![]() ,则
,则![]() 为二面角
为二面角![]() 的一个平面角.由此利用二面角
的一个平面角.由此利用二面角![]() 的余弦值为余弦值为
的余弦值为余弦值为![]() ,可求实数
,可求实数![]() 的值.
的值.
试题解析:(Ⅰ)证明,连接![]() 交
交![]() 于
于![]() ,则
,则![]() 为
为![]() 的中点
的中点
连接![]() ,则
,则![]() ,而
,而![]() 平面
平面![]()
所以![]() 平面
平面![]() ;
;
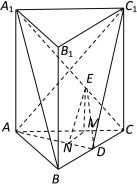
(Ⅱ)方法一:过![]() 作
作![]()
![]()
![]() 于
于![]() ,则
,则![]()
![]() 平面
平面![]() ,过
,过![]() 作
作![]()
![]()
![]() ,垂足为
,垂足为![]() ,连
,连![]() ,则
,则![]()
![]()
![]() ,所以
,所以![]() 为二面角
为二面角![]() 的一个平面角.
的一个平面角.
设![]() ,则
,则![]() ,所以
,所以![]() ,所以
,所以![]()
因为![]() , 所以
, 所以![]()
故![]()
因![]() ,故
,故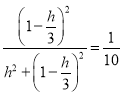 ,解得
,解得![]()
此时, 点![]() 为
为![]() 的中点,所以
的中点,所以![]()
方法二:建立如图所示空间直角坐标系,过![]() 作
作![]() 于
于![]() ,则
,则![]() 平面
平面![]() ,设
,设![]() ,则
,则![]() ,
, 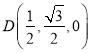 ,
, ![]() ,所以
,所以![]() ,
, 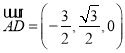
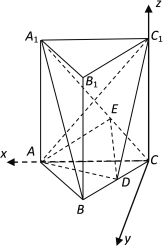
依题意![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
设![]() 为平面
为平面![]() 一个法向量,
一个法向量,
则由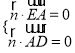 可得
可得![]()
所以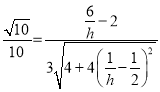 解得
解得![]() ,所以
,所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列说法:
①y=sinx+cosx在区间(﹣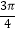 ,
,  )内单调递增;
)内单调递增;
②存在实数α,使sinαcosα= ;
;
③y=sin( +2x)是奇函数;
+2x)是奇函数;
④x= 是函数y=cos(2x+
是函数y=cos(2x+ 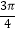 )的一条对称轴方程.
)的一条对称轴方程.
其中正确说法的序号是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关注的话题,为了解公众对“延迟退休”的态度,某校课外研究性学习小组在某社区随机抽取了50人进行调查,将调查情况进行整理后制成下表:
年龄
[20,25)
[25,30)
[30,35)
[35,40)
[40,45)
人数
4
5
8
5
3
年龄
[45,50)
[50,55)
[55,60)
[60,65)
[65,70)
人数
6
7
3
5
4
经调查年龄在[25,30),[55,60)的被调查者中赞成“延迟退休”的人数分别是3人和2人.现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(I)求年龄在[25,30)的被调查者中选取的2人都赞成“延迟退休”的概率;
(II)若选中的4人中,不赞成“延迟退休”的人数为
 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
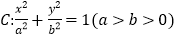 经过点
经过点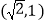 ,且离心率为
,且离心率为 .
.(Ⅰ)求椭圆
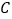 的方程;
的方程;(Ⅱ)设
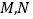 是椭圆上的点,直线
是椭圆上的点,直线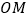 与
与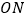 (
(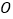 为坐标原点)的斜率之积为
为坐标原点)的斜率之积为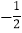 .若动点
.若动点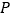 满足
满足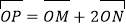 ,试探究是否存在两个定点
,试探究是否存在两个定点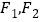 ,使得
,使得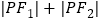 为定值?若存在,求
为定值?若存在,求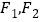 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】“累积净化量
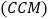 ”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据
”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据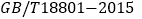 《空气净化器》国家标准,对空气净化器的累计净化量
《空气净化器》国家标准,对空气净化器的累计净化量 有如下等级划分:
有如下等级划分:累积净化量(克)
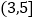
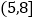
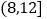
12以上
等级
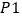
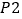
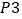
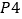
为了了解一批空气净化器(共5000台)的质量,随机抽取
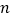 台机器作为样本进行估计,已知这
台机器作为样本进行估计,已知这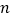 台机器的累积净化量都分布在区间
台机器的累积净化量都分布在区间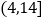 中,按照
中,按照 、
、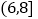 、
、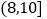 、
、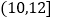 、
、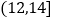 均匀分组,其中累积净化量在
均匀分组,其中累积净化量在 的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示: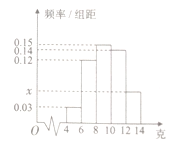
(1)求
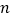 的值及频率分布直方图中
的值及频率分布直方图中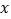 的值;
的值;(2)以样本估计总体,试估计这批空气净化器(共5000台)中等级为
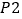 的空气净化器有多少台?
的空气净化器有多少台?(3)从累积净化量在
 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为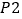 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
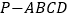 中,底面
中,底面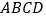 是边长为
是边长为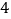 的菱形,
的菱形,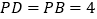 ,
,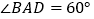 ,
,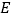 为
为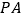 中点.
中点.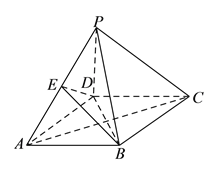
(1)求证:平面
 平面
平面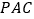 ;
;(2)若
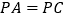 ,
,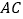 ,
,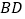 的交点记为
的交点记为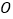 ,求证
,求证 平面
平面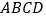 ;
;(3)在(2)的条件下求三棱锥
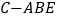 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
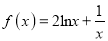 .
.(1)讨论函数
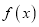 的单调性;
的单调性;(2)如果对所有的
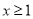 ,都有
,都有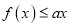 ,求
,求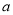 的取值范围.
的取值范围.
相关试题

