【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的极值和单调区间;
的极值和单调区间;
(2)若在区间![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() 取得极小值为
取得极小值为![]() ,
,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
(2)![]()
![]() .
.
【解析】
(1)求函数![]() 的导数,令导数等于零,解方程,再求出函数
的导数,令导数等于零,解方程,再求出函数![]() 的导数和驻点,然后列表讨论,求函数
的导数和驻点,然后列表讨论,求函数![]() 的单调区间和极值;
的单调区间和极值;
(2)若在区间![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,其充要条件是
成立,其充要条件是![]() 在区间
在区间![]() 上的最小值小于
上的最小值小于![]() 即可.利用导数研究函数在区间
即可.利用导数研究函数在区间![]() 上的最小值,先求出导函数
上的最小值,先求出导函数![]() ,然后讨论研究函数在
,然后讨论研究函数在![]() 上的单调性,将
上的单调性,将![]() 的极值点与区间
的极值点与区间![]() 的端点比较,确定其最小的极值点.
的端点比较,确定其最小的极值点.
解:![]() 的定义域为
的定义域为![]() ,
,
因为![]() ,
,
(1)当![]() 时,
时,![]() ,令
,令![]() ,得
,得![]() ,
,
又![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,![]() 随
随![]() 的变化情况如下表:
的变化情况如下表:
|
| 1 |
|
|
| 0 |
|
| 单调递减 | 极小值 | 单调递增 |
所以![]() 时,
时,![]() 取得极小值为
取得极小值为![]() .
.
![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)因为![]() ,且
,且![]() .
.
令![]() ,得
,得![]() ,
,
若在区间![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,
成立,
其充要条件是![]() 在区间
在区间![]() 上的最小值小于0即可.
上的最小值小于0即可.
![]() 当
当![]() ,即
,即![]() 时,
时,![]() 对
对![]() 成立,
成立,
所以,![]() 在区间
在区间![]() 上单调递减,
上单调递减,
故![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
由![]() ,得
,得![]() ,即
,即![]() .
.
![]() 当
当![]() ,即
,即![]() 时,
时,
若![]() ,则
,则![]() 对
对![]() 成立,
成立,
所以![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以,![]() 在区间
在区间![]() 上的最小值为
上的最小值为
![]() ,
,
显然,![]() 在区间
在区间![]() 上的最小值小于
上的最小值小于![]() 不成立.
不成立.
若![]() ,即
,即![]() 时,则有
时,则有
|
|
|
|
|
|
|
|
| 单调递减 | 极小值 | 单调递增 |
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
由![]() ,
,
得![]() ,解得
,解得![]() ,即
,即![]() .
.
综上,由![]()
![]() 可知
可知![]()
![]() 符合题意.
符合题意.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段
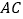 、
、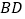 交于点
交于点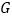 ,在
,在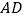 的延长线上任取一点
的延长线上任取一点 ,得凸四边形
,得凸四边形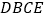 ,求证:
,求证: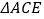 、
、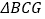 、
、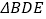 的外接圆三圆共点。
的外接圆三圆共点。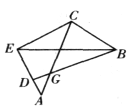
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
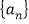 的前
的前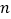 项和为
项和为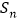 ,
,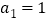 且
且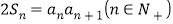 。
。(1)证明:
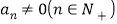 ,并求
,并求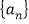 的通项公式;
的通项公式;(2)构造数列
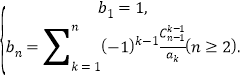 求证:无论给定多么大的正整数
求证:无论给定多么大的正整数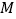 ,都必定存在一个
,都必定存在一个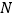 ,使
,使 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,
中, 是正三角形,四边形
是正三角形,四边形 是菱形,点
是菱形,点 是
是 的中点.
的中点.
(I)求证:
 // 平面
// 平面 ;
;(II)若平面
 平面
平面 ,
, , 求直线
, 求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,曲线
 与坐标轴的交点都在圆C上.
与坐标轴的交点都在圆C上.(1)求圆C的方程;
(2)若圆C与直线
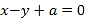 交于A,B两点,且
交于A,B两点,且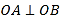 ,求a的值.
,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】新高考方案的实施,学生对物理学科的选择成了焦点话题. 某学校为了了解该校学生的物理成绩,从
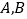 ,两个班分别随机调查了40名学生,根据学生的某次物理成绩,得到
,两个班分别随机调查了40名学生,根据学生的某次物理成绩,得到 班学生物理成绩的频率分布直方图和
班学生物理成绩的频率分布直方图和 班学生物理成绩的频数分布条形图.
班学生物理成绩的频数分布条形图.
(Ⅰ)估计
 班学生物理成绩的众数、中位数(精确到
班学生物理成绩的众数、中位数(精确到 )、平均数(各组区间内的数据以该组区间的中点值为代表);
)、平均数(各组区间内的数据以该组区间的中点值为代表);(Ⅱ)填写列联表,并判断是否有
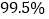 的把握认为物理成绩与班级有关?
的把握认为物理成绩与班级有关?物理成绩
 的学生数
的学生数物理成绩
 的学生数
的学生数合计
 班
班 班
班合计
附:
 列联表随机变量
列联表随机变量 ;
;
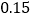




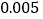

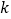
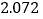


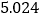
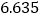


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
: (
( )的左、右焦点分别为
)的左、右焦点分别为 ,过点
,过点 的直线
的直线 交
交 于
于 ,
, 两点,
两点, 的周长为
的周长为 ,
,  的离心率
的离心率
(Ⅰ)求
 的方程;
的方程;(Ⅱ)设点
 ,
, ,过点
,过点 作
作 轴的垂线
轴的垂线 ,试判断直线
,试判断直线 与直线
与直线 的交点是否恒在一条定直线上?若是,求该定直线的方程;否则,说明理由.
的交点是否恒在一条定直线上?若是,求该定直线的方程;否则,说明理由.
相关试题

