【题目】已知椭圆![]() :
:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,过点
,过点![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,
两点,![]() 的周长为
的周长为![]() ,
, ![]() 的离心率
的离心率![]()
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,试判断直线
,试判断直线![]() 与直线
与直线![]() 的交点是否恒在一条定直线上?若是,求该定直线的方程;否则,说明理由.
的交点是否恒在一条定直线上?若是,求该定直线的方程;否则,说明理由.
参考答案:
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】
(I)由![]() 的周长为
的周长为![]() 求得椭圆的a,再离心率
求得椭圆的a,再离心率![]() ,然后求得椭圆的方程;
,然后求得椭圆的方程;
(II)设直线l:x=my+4,![]() ,联立方程,运用韦达定理,再写出直线BD的方程为:
,联立方程,运用韦达定理,再写出直线BD的方程为:![]() 与
与![]() 的交点,最后求解计算出
的交点,最后求解计算出![]() 与m无关,得出答案.
与m无关,得出答案.
解:(I)由椭圆的定义,![]() 的周长为
的周长为![]() ,即4a=20,解得a=5,
,即4a=20,解得a=5,
又椭圆![]() 的离心率
的离心率![]() ,解得c=4
,解得c=4
所以![]()
所以椭圆方程![]() ;
;
(II)显然过点![]() 的直线l不垂直y轴,设l:x=my+4,
的直线l不垂直y轴,设l:x=my+4,![]()
联立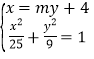 ,得
,得![]()
韦达定理:![]()
直线![]() 的方程为
的方程为![]()
直线BD的方程为:![]()
解得![]()
又点![]() 在直线l上,所以
在直线l上,所以![]()
再代入解得![]()
又![]()
代入解得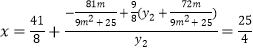 (与m无关)
(与m无关)
故直线![]() 与直线BD的交点恒落在直线
与直线BD的交点恒落在直线![]() 上.
上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
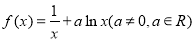 .
.(1)若
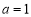 ,求函数
,求函数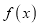 的极值和单调区间;
的极值和单调区间;(2)若在区间
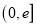 上至少存在一点
上至少存在一点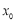 ,使得
,使得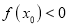 成立,求实数
成立,求实数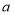 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,曲线
 与坐标轴的交点都在圆C上.
与坐标轴的交点都在圆C上.(1)求圆C的方程;
(2)若圆C与直线
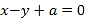 交于A,B两点,且
交于A,B两点,且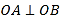 ,求a的值.
,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】新高考方案的实施,学生对物理学科的选择成了焦点话题. 某学校为了了解该校学生的物理成绩,从
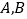 ,两个班分别随机调查了40名学生,根据学生的某次物理成绩,得到
,两个班分别随机调查了40名学生,根据学生的某次物理成绩,得到 班学生物理成绩的频率分布直方图和
班学生物理成绩的频率分布直方图和 班学生物理成绩的频数分布条形图.
班学生物理成绩的频数分布条形图.
(Ⅰ)估计
 班学生物理成绩的众数、中位数(精确到
班学生物理成绩的众数、中位数(精确到 )、平均数(各组区间内的数据以该组区间的中点值为代表);
)、平均数(各组区间内的数据以该组区间的中点值为代表);(Ⅱ)填写列联表,并判断是否有
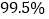 的把握认为物理成绩与班级有关?
的把握认为物理成绩与班级有关?物理成绩
 的学生数
的学生数物理成绩
 的学生数
的学生数合计
 班
班 班
班合计
附:
 列联表随机变量
列联表随机变量 ;
;
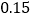




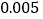

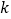
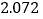


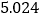
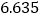


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,点
中,点 ,直线
,直线 ,设圆
,设圆 的半径为1, 圆心在
的半径为1, 圆心在 上.
上.
(1)若圆心
 也在直线
也在直线 上,过点
上,过点 作圆
作圆 的切线,求切线方程;
的切线,求切线方程;(2)若圆
 上存在点
上存在点 ,使
,使 ,求圆心
,求圆心 的横坐标
的横坐标 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
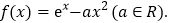
(I)求函数
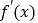 的极值;
的极值;(II)若方程
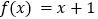 仅有一个实数解,求
仅有一个实数解,求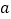 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80 m.经测量,点A位于点O正北方向60 m处,点C位于点O正东方向170 m处(OC为河岸),tan∠BCO=
 .
.
(1)求新桥BC的长;
(2)当OM多长时,圆形保护区的面积最大?
相关试题

