【题目】新高考方案的实施,学生对物理学科的选择成了焦点话题. 某学校为了了解该校学生的物理成绩,从![]() ,两个班分别随机调查了40名学生,根据学生的某次物理成绩,得到
,两个班分别随机调查了40名学生,根据学生的某次物理成绩,得到![]() 班学生物理成绩的频率分布直方图和
班学生物理成绩的频率分布直方图和![]() 班学生物理成绩的频数分布条形图.
班学生物理成绩的频数分布条形图.

(Ⅰ)估计![]() 班学生物理成绩的众数、中位数(精确到
班学生物理成绩的众数、中位数(精确到![]() )、平均数(各组区间内的数据以该组区间的中点值为代表);
)、平均数(各组区间内的数据以该组区间的中点值为代表);
(Ⅱ)填写列联表,并判断是否有![]() 的把握认为物理成绩与班级有关?
的把握认为物理成绩与班级有关?
物理成绩 | 物理成绩 | 合计 | |
| |||
| |||
合计 |
附:![]() 列联表随机变量
列联表随机变量![]() ;
;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考答案:
【答案】(I)![]() ;(II)有.
;(II)有.
【解析】
(Ⅰ)直接根据频率分布直方图,求得各个组的概率,利用公式求得众数、中位数和平均数;
(II)利用频率分布直方图填写列联表,然后求![]() ,即可判断出是否有
,即可判断出是否有![]() 的把握认为物理成绩与班级有关.
的把握认为物理成绩与班级有关.
(Ⅰ)估计A班学生物理成绩的总数为:![]()
由左至右各个分区间的概率分别为0.1,0.2,0.3,0.2,0.15,0.05
中位数60+![]()
平均数:![]()
(Ⅱ)
物理成绩 | 物理成绩 | 合计 | |
| 24 | 16 | 40 |
| 10 | 30 | 40 |
合计 | 34 | 46 | 80 |
![]()
所以有![]() 的把握认为物理成绩与班级有关
的把握认为物理成绩与班级有关
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,
中, 是正三角形,四边形
是正三角形,四边形 是菱形,点
是菱形,点 是
是 的中点.
的中点.
(I)求证:
 // 平面
// 平面 ;
;(II)若平面
 平面
平面 ,
, , 求直线
, 求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
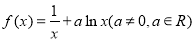 .
.(1)若
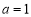 ,求函数
,求函数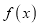 的极值和单调区间;
的极值和单调区间;(2)若在区间
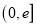 上至少存在一点
上至少存在一点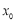 ,使得
,使得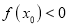 成立,求实数
成立,求实数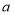 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,曲线
 与坐标轴的交点都在圆C上.
与坐标轴的交点都在圆C上.(1)求圆C的方程;
(2)若圆C与直线
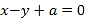 交于A,B两点,且
交于A,B两点,且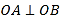 ,求a的值.
,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
: (
( )的左、右焦点分别为
)的左、右焦点分别为 ,过点
,过点 的直线
的直线 交
交 于
于 ,
, 两点,
两点, 的周长为
的周长为 ,
,  的离心率
的离心率
(Ⅰ)求
 的方程;
的方程;(Ⅱ)设点
 ,
, ,过点
,过点 作
作 轴的垂线
轴的垂线 ,试判断直线
,试判断直线 与直线
与直线 的交点是否恒在一条定直线上?若是,求该定直线的方程;否则,说明理由.
的交点是否恒在一条定直线上?若是,求该定直线的方程;否则,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
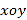 中,点
中,点 ,直线
,直线 ,设圆
,设圆 的半径为1, 圆心在
的半径为1, 圆心在 上.
上.
(1)若圆心
 也在直线
也在直线 上,过点
上,过点 作圆
作圆 的切线,求切线方程;
的切线,求切线方程;(2)若圆
 上存在点
上存在点 ,使
,使 ,求圆心
,求圆心 的横坐标
的横坐标 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
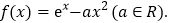
(I)求函数
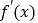 的极值;
的极值;(II)若方程
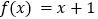 仅有一个实数解,求
仅有一个实数解,求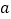 的取值范围.
的取值范围.
相关试题

