【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 且
且![]() 。
。
(1)证明:![]() ,并求
,并求![]() 的通项公式;
的通项公式;
(2)构造数列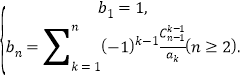 求证:无论给定多么大的正整数
求证:无论给定多么大的正整数![]() ,都必定存在一个
,都必定存在一个![]() ,使
,使![]() .
.
参考答案:
【答案】(1)见解析;(2)见解析
【解析】
(1)由![]() 及
及![]() ,得
,得![]() 。由
。由![]() ,
,![]() 及
及![]() ,得
,得![]() 。
。
下面用数学归纳法证明:![]() ,即
,即![]()
![]() .①
.①
(i)当![]() 时,由
时,由![]() ,
,![]() ,知①成立。
,知①成立。
(ii)假设![]() 时,①成立,即
时,①成立,即![]() ,
,![]() ,有
,有![]() ,约去
,约去![]() 得
得![]() .移项并代入
.移项并代入![]() 得
得![]()
![]()
![]() .②则
.②则![]()
![]() 。
。
约去![]() 得
得![]() .约去
.约去![]() 得
得![]() ,
,
移项并代入![]() 得
得![]() .②由式②、③知,当
.②由式②、③知,当![]() 时,①成立,综上得证式①成立。
时,①成立,综上得证式①成立。
合并得![]() ,这就证明了
,这就证明了![]() ,且求出了通项
,且求出了通项![]() 。
。
(2)把![]() 代入,对
代入,对![]() 有
有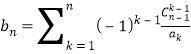
![]()
![]()
![]()
![]()
![]() 。
。
因为![]()
![]() ,
,
所以,对于给定的正整数![]() ,存在一个
,存在一个![]() ,使
,使![]()
![]()
![]()
![]() 。
。
说明:第(1)问用公式![]() 可得
可得![]()
![]() ,
,
但需![]() ,才能推出
,才能推出![]() ,
,
此解法特点是“证明![]() ,并求
,并求![]() 的通项公式”同时进行。
的通项公式”同时进行。
第(2)问的一个背景是调和级数![]() 发散,证明不是唯一的。
发散,证明不是唯一的。
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面一道题目的证明,指出其中的一处错误。题目:平面上有六个点,任何三点都是三边互不相等三角形的顶点,则这些三角形中有一个的最短边又是另一个三角形的最长边。证明:第一步,对已知的六个点作两两连线,可以得出15条边,记为
 ,
, ,…,
,…, .第二步,由于任何三点组成的都是“三边互不相等的三角形”,因此,15条边互不相等不妨设
.第二步,由于任何三点组成的都是“三边互不相等的三角形”,因此,15条边互不相等不妨设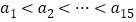 .第三步,由于“任何三点都是三边互不相等三角形的顶点”,因此,任取三条边都可以组成三角形,则
.第三步,由于“任何三点都是三边互不相等三角形的顶点”,因此,任取三条边都可以组成三角形,则 、
、 、
、 组成的三角形的最长边
组成的三角形的最长边 ,也是
,也是 、
、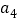 、
、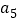 组成的三角形的最短边,命题得证.这三步中,第______步有错误,理由是______.
组成的三角形的最短边,命题得证.这三步中,第______步有错误,理由是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的类比过程。
(1)在一维直线上,线段是一个封闭的中心对称图形,有命题1:不重合的两点决定一条线段;
(2)在二维平面上,圆是一个封闭的中心对称图形,有命题2:不共线的三点决定一个圆;
(3)在三维空间中,球是一个封闭的中心对称图形,类比猜想:不共面的四点决定一个球。
证明或否定这个类比猜想:不共面的四点决定一个球。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段
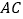 、
、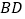 交于点
交于点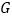 ,在
,在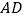 的延长线上任取一点
的延长线上任取一点 ,得凸四边形
,得凸四边形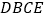 ,求证:
,求证: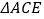 、
、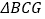 、
、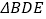 的外接圆三圆共点。
的外接圆三圆共点。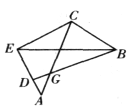
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,
中, 是正三角形,四边形
是正三角形,四边形 是菱形,点
是菱形,点 是
是 的中点.
的中点.
(I)求证:
 // 平面
// 平面 ;
;(II)若平面
 平面
平面 ,
, , 求直线
, 求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
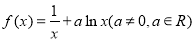 .
.(1)若
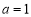 ,求函数
,求函数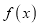 的极值和单调区间;
的极值和单调区间;(2)若在区间
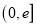 上至少存在一点
上至少存在一点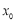 ,使得
,使得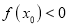 成立,求实数
成立,求实数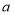 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,曲线
 与坐标轴的交点都在圆C上.
与坐标轴的交点都在圆C上.(1)求圆C的方程;
(2)若圆C与直线
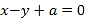 交于A,B两点,且
交于A,B两点,且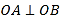 ,求a的值.
,求a的值.
相关试题

