【题目】在平面直角坐标系中,曲线![]() 与坐标轴的交点都在圆C上.
与坐标轴的交点都在圆C上.
(1)求圆C的方程;
(2)若圆C与直线![]() 交于A,B两点,且
交于A,B两点,且![]() ,求a的值.
,求a的值.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)求出曲线![]() 与坐标轴的三个交点,根据这三个交点在圆上可求出圆心坐标和半径,从而可得圆的方程;
与坐标轴的三个交点,根据这三个交点在圆上可求出圆心坐标和半径,从而可得圆的方程;
(2)设A![]() ,B
,B![]() ,联立直线与圆的方程,根据根与系数的关系可得
,联立直线与圆的方程,根据根与系数的关系可得![]() ,
,![]() ,根据
,根据![]() 得
得![]() ,化为
,化为![]() ,进而可解得
,进而可解得![]() .
.
(1)曲线![]() 与坐标轴的交点为(0,1),(
与坐标轴的交点为(0,1),(![]() ,0),
,0),
由题意可设圆C的圆心坐标为(3,![]() ),
),
∴![]() ,解得
,解得![]() ,
,
∴圆C的半径为![]() ,
,
∴圆C的方程为![]() .
.
(2)设点A、B的坐标分别为A![]() ,B
,B![]() ,其坐标满足方程组
,其坐标满足方程组![]() ,消去
,消去![]() 得到方程
得到方程![]() ,
,
由已知得,判别式![]() ①,
①,
由根与系数的关系得![]() ,
,![]() ②,
②,
由![]() 得
得![]() .
.
又∵![]() ,
,![]() ,∴
,∴![]() 可化为
可化为![]() ③,
③,
将②代入③解得![]() ,经检验,
,经检验,![]() 满足①,即
满足①,即![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
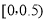 ,
,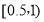 ,…,
,…,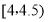 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.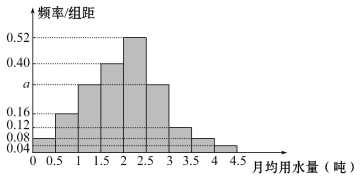
(1)求直方图中a的值.
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由.
(3)若该市政府希望使85%的居民每月的用水量不超过标准x(吨),估计x的值,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先后2次抛掷一枚骰子,将得到的点数分别记为
 ,
, .
.(1)求直线
 与圆
与圆 相切的概率;
相切的概率;(2)将
 ,
, ,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
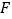 是抛物线
是抛物线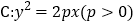 的焦点,若点
的焦点,若点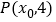 在抛物线
在抛物线 上,且
上,且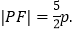
 求抛物线
求抛物线 的方程;
的方程; 动直线
动直线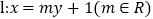 与抛物线
与抛物线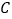 相交于
相交于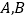 两点,问:在
两点,问:在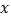 轴上是否存在定点
轴上是否存在定点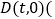 其中
其中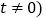 ,使得向量
,使得向量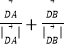 与向量
与向量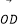 共线
共线 其中
其中 为坐标原点
为坐标原点 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
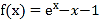 (
(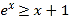 是自然对数的底数)
是自然对数的底数)(1)求证:
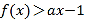
(2)若不等式
 在
在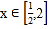 上恒成立,求正数
上恒成立,求正数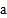 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程
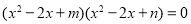 的四个根组成一个首项为
的四个根组成一个首项为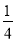 的等差数列,则
的等差数列,则 _____.
_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CM,CN为某公园景观湖胖的两条木栈道,∠MCN=120°,现拟在两条木栈道的A,B处设置观景台,记BC=a,AC=b,AB=c(单位:百米)
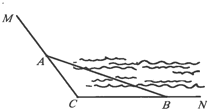
(1)若a,b,c成等差数列,且公差为4,求b的值;
(2)已知AB=12,记∠ABC=θ,试用θ表示观景路线A-C-B的长,并求观景路线A-C-B长的最大值.
相关试题

