【题目】已知函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,函数
上单调递增,函数 .
.
(1)请写出函数![]() 与函数
与函数![]() 在
在![]() 的单调区间(只写结论,不证明);
的单调区间(只写结论,不证明);
(2)求函数![]() 的最值;
的最值;
(3)讨论方程![]() 实根的个数.
实根的个数.
参考答案:
【答案】(1)函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ,函数
,函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ;(2)最小值
;(2)最小值![]() ,最大值
,最大值![]() ;(3)当
;(3)当![]() 时,方程实根个数为
时,方程实根个数为![]() ,当
,当![]() 时,方程实根个数为
时,方程实根个数为![]() ,当
,当![]() 时,方程实根个数为
时,方程实根个数为![]() ,当
,当![]() 时,方程实根个数为
时,方程实根个数为![]() ,当
,当![]() 时,方程实根个数为
时,方程实根个数为![]() .
.
【解析】
试题分析:(1)令![]() ,通过类比可知
,通过类比可知![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ,同理,令
,同理,令![]() ,通过类比可得函数
,通过类比可得函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ;(2)化简
;(2)化简![]() ,由(1)可知,
,由(1)可知,![]() 与
与![]() 均在
均在![]() 单调递减,在
单调递减,在![]() 上单调递增,由此求得最大值和最小值;(3)对原方程因式分解得
上单调递增,由此求得最大值和最小值;(3)对原方程因式分解得![]() ,所以
,所以![]() 或
或![]() ,下面对
,下面对![]() 进行分类讨论函数的零点的情况.
进行分类讨论函数的零点的情况.
试题解析:
(1)根据条件,
![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ,
,
函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ;
;
(2)![]() ,
,
由(1)可知,![]() 与
与![]() 均在
均在![]() 单调递减,在
单调递减,在![]() 上单调递增,
上单调递增,
则有函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
![]() ;
;
(3)由![]() 可得
可得![]() ,所以有
,所以有![]() 或
或![]() ,又函数
,又函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,而
单调递增,而![]() ,
,
所以当![]() 时,方程无实数根;
时,方程无实数根;
当![]() 时,有一个实数根;
时,有一个实数根;
当![]() ,且
,且![]() 即
即![]() ,方程有两个实数根;
,方程有两个实数根;
当![]() ,方程有三个实数根;
,方程有三个实数根;
当![]() 时,方程有四个实数根,
时,方程有四个实数根,
综上,①当![]() 时,方程实根个数为0;
时,方程实根个数为0;
②当![]() 时,方程实根个数为1;
时,方程实根个数为1;
③当![]() 时,方程实根个数为2;
时,方程实根个数为2;
④当![]() 时,方程实根个数为3;
时,方程实根个数为3;
⑤当![]() 时,方程实根个数为4.
时,方程实根个数为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
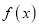 的定义域为
的定义域为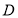 ,若存在闭区间
,若存在闭区间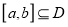 ,使得函数
,使得函数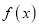 满足:①
满足:①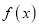 在
在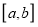
上是单调函数;②
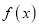 在
在 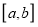 上的值域是
上的值域是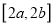 ,则称区间
,则称区间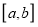 是函数
是函数 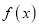 的“和谐区间”,
的“和谐区间”,下列结论错误的是( )
A.函数
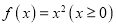 存在 “和谐区间”
存在 “和谐区间”B.函数
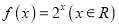 存在 “和谐区间”
存在 “和谐区间”C.函数
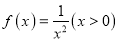 不存在 “和谐区间”
不存在 “和谐区间”D.函数
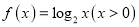 存在 “和谐区间”
存在 “和谐区间” -
科目: 来源: 题型:
查看答案和解析>>【题目】设
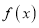 是定义在
是定义在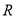 上的函数,对任意实数
上的函数,对任意实数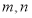 ,,都有
,,都有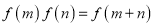 ,且当
,且当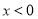 时,
时,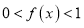 .
.(1)证明:①
 ;②当
;②当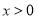 时,
时,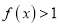 ;③
;③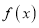 是
是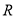 上的增函数;
上的增函数;(2)设
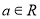 ,试解关于
,试解关于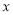 的不等式
的不等式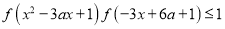 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,已知cos Acos B>sin Asin B,则△ABC是( )
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
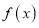 满足
满足 ,且
,且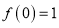 .
.(1)求
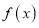 的解析式;
的解析式;(2)若函数
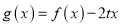 在区间
在区间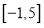 上是单调函数,求实数
上是单调函数,求实数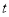 的取值范围;
的取值范围;(3)若关于
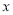 的方程
的方程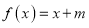 有区间
有区间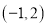 上有唯一实数根,求实数
上有唯一实数根,求实数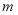 的取值范围.
的取值范围.(注:相等的实数根算一个).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
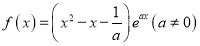 .
.(Ⅰ)当
 时,求函数
时,求函数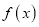 的零点;
的零点;(Ⅱ)求
 的单调区间;
的单调区间;(Ⅲ)当
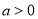 时,若
时,若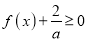 对
对 恒成立,求
恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】集合M={1,3,a},N={2,a2}.若M∪N={1,2,3,4,16},则a的值为( )
A.0
B.1
C.2
D.4
相关试题

