【题目】设函数![]() 的定义域为
的定义域为![]() ,若存在闭区间
,若存在闭区间![]() ,使得函数
,使得函数![]() 满足:①
满足:①![]() 在
在![]()
上是单调函数;②![]() 在
在 ![]() 上的值域是
上的值域是![]() ,则称区间
,则称区间![]() 是函数
是函数 ![]() 的“和谐区间”,
的“和谐区间”,
下列结论错误的是( )
A.函数 ![]() 存在 “和谐区间”
存在 “和谐区间”
B.函数 ![]() 存在 “和谐区间”
存在 “和谐区间”
C.函数 ![]() 不存在 “和谐区间”
不存在 “和谐区间”
D.函数 ![]() 存在 “和谐区间”
存在 “和谐区间”
参考答案:
【答案】D
【解析】
试题分析:A中,当![]() 时,
时,![]() 在
在![]() 上是单调增函数,且
上是单调增函数,且![]() 在
在![]() 上的值域是
上的值域是![]() ,∴存在“和谐区间”,原命题正确;B中,当
,∴存在“和谐区间”,原命题正确;B中,当![]() 时,
时,![]() 在
在![]() 上是单调增函数,且
上是单调增函数,且![]() 在
在![]() 上的值域是
上的值域是![]() ,∴存在“和谐区间”,原命题正确;C中,
,∴存在“和谐区间”,原命题正确;C中,![]() 是单调减函数,且
是单调减函数,且![]() 在
在![]() 上的值域是
上的值域是![]() ,∴不存在“和谐区间”,原命题正确;D中,当
,∴不存在“和谐区间”,原命题正确;D中,当![]() 时,
时,![]() 是单调增函数,假设存在
是单调增函数,假设存在![]() 满足题意,则
满足题意,则![]() ,且
,且![]() ,即
,即![]() ,且
,且![]() ;∴
;∴![]() ,且
,且![]() ,即
,即![]() ,且
,且![]() ;这与函数的单调性矛盾,∴假设不成立,即函数不存在“和谐区间”,原命题不正确;故选D.
;这与函数的单调性矛盾,∴假设不成立,即函数不存在“和谐区间”,原命题不正确;故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成的.已知半球的直径是6 cm,圆柱筒高为2 cm.

(1)这种“浮球”的体积是多少cm3(结果精确到0.1)?
(2)要在2 500个这样的“浮球”表面涂一层胶,如果每平方米需要涂胶100克,那么共需胶多少克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 满足
满足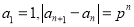 ,其中
,其中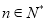 ,
,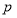 是不为1的常数.
是不为1的常数.(Ⅰ)证明:若
 是递增数列,则
是递增数列,则 不可能是等差数列;
不可能是等差数列;(Ⅱ)证明:若
 是递减的等比数列,则
是递减的等比数列,则 中的每一项都大于其后任意
中的每一项都大于其后任意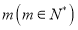 个项的和;
个项的和;(Ⅲ)若
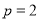 ,且
,且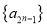 是递增数列,
是递增数列,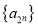 是递减数列,求数列
是递减数列,求数列 的通项公式.
的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据统计资料,某工艺品厂的日产量最多不超过20件根据统计资料,每日产品废品率
 与日产量
与日产量 (件)之间近似地满足关系式
(件)之间近似地满足关系式 (日产品废品率=
(日产品废品率= ×100%) .已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润
×100%) .已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润 日正品赢利额
日正品赢利额 日废品亏损额)
日废品亏损额) (1)将该车间日利润
 (千元)表示为日产量
(千元)表示为日产量 (件)的函数;
(件)的函数;(2)当该车间的日产量为多少件时,日利润最大?最大日利润是几千元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
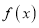 是定义在
是定义在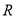 上的函数,对任意实数
上的函数,对任意实数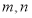 ,,都有
,,都有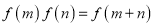 ,且当
,且当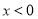 时,
时,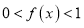 .
.(1)证明:①
 ;②当
;②当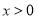 时,
时,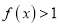 ;③
;③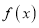 是
是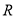 上的增函数;
上的增函数;(2)设
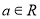 ,试解关于
,试解关于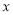 的不等式
的不等式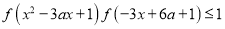 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,已知cos Acos B>sin Asin B,则△ABC是( )
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
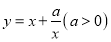 在区间
在区间 上单调递减,在区间
上单调递减,在区间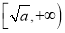 上单调递增,函数
上单调递增,函数 .
.(1)请写出函数
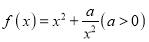 与函数
与函数 在
在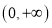 的单调区间(只写结论,不证明);
的单调区间(只写结论,不证明);(2)求函数
 的最值;
的最值;(3)讨论方程
 实根的个数.
实根的个数.
相关试题

