搜索
【题目】(本小题13分)已知函数f(x)＝
－
(a>0，x>0)．
(1)求证：f(x)在(0，＋∞)上是单调递增函数；
(2)若f(x)在[
，2]上的值域是[
，2]，求a的值．
参考答案：
【答案】(1)证明：见解析；(2) a＝
.
【解析】本事主要是考查了函数的单调性和函数值域的求解的综合运用。
（1）先分析函数的定义域内任意两个变量，代入函数解析式中作差，然后变形定号，下结论。
（2）∵f(x)在[
，2]上的值域是[
，2]，那么可知又f(x)在[
，2]上单调递增，可知最大值和最小值在端点值取得求解得到参数a的值。
解：(1)证明：设x2>x1>0，则x2－x1>0，x1x2>0.
∵f(x2)－f(x1)＝(
－
)－( 
－
)＝
－
＝
>0，
∴f(x2)>f(x1)，∴f(x)在(0，＋∞)上是单调递增的．………………6分
(2)∵f(x)在[，2]上的值域是[，2]，
又f(x)在[，2]上单调递增，∴f(
)＝
，f(2)＝2，
易得a＝. ………………13分
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店销售10台A型和20台B型电脑的利润为4000元，销售20台A型和10台B型电脑的利润为3500元．
（1)求每台A型电脑和B型电脑的销售利润；
（2）该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍。设购进A掀电脑x台，这100台电脑的销售总利润为y元。
①求y与x的关系式；
②该商店购进A型、B型各多少台，才能使销售利润最大？
（3）实际进货时，厂家对A型电脑出厂价下调m（0＜m＜100）元，且限定商店最多购进A型电脑70台。若商店保持两种电脑的售价不变，请你以上信息及（2）中的条件，设计出使这100台电脑销售总利润最大的进货方案。
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直角坐标系
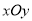中，曲线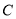
的参数方程为
（
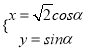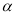为参数），以原点
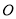为极点，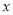 
轴正半轴为极轴，建立极坐标系，直线
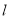的极坐标方程为
．（1）求曲线
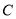的普通方程与直线
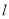的直角坐标方程；（2）设
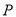为曲线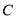
上的动点，求点
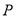的直线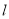
的距离的最小值. -
科目： 来源： 题型：
查看答案和解析>>【题目】为了研究“教学方式”对教学质量的影响，某高中老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学（勤奋程度和自觉性都一样）．以下茎叶图为甲、乙两班（每班均为20人）学生的数学期末考试成绩．
（1）现从甲班数学成绩不低于80分的同学中随机抽取两名同学，求成绩为87分的同学至少有一名被抽中的概率；
（2）学校规定：成绩不低于75分的为优秀，请填写下面的
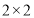列联表，并判断有多大把握认为“成绩优秀与教学方式有关”．甲班
乙班
合计
优秀
不优秀
合计
下面临界值表供参考：
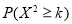
0.15
0.10
0.05
0.025
0.010
0.005
0.001
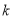
span>2.072
2.706
3.841
5.024
6.635
7.879
10.828
（参考公式：
） -
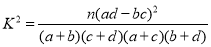科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线
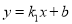与反比例函数
的图象交于B、C两点，B（2，m）且m＜2，正方形ABCD的顶点A、D在坐标轴上。⑴ 求
， 
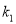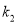的值；⑵ 直接写出
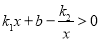时，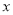 
的取值范围。 
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法中，正确的有( )
①函数y＝
的定义域为{x|x≥1}；②函数y＝x2＋x＋1在(0，＋∞)上是增函数；
③函数f(x)＝x3＋1(x∈R)，若f(a)＝2，则f(－a)＝－2；
④已知f(x)是R上的增函数，若a＋b>0，则有f(a)＋f(b)>f(－a)＋f(－b)．
A. 0个 B. 1个 C. 2个 D. 3个
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f(x)的定义域为(－2,2)，函数g(x)＝f(x－1)＋f(3－2x)．
(1)求函数g(x)的定义域；
(2)若f(x)是奇函数，且在定义域上单调递减，求不等式g(x)≤0的解集．
相关试题
