搜索
【题目】已知等差数列{an}的前3项和为6，前8项和为－4.
(1)求数列{an}的通项公式；
(2)设bn＝(4－an)qn－1 (q≠0，n∈N*)，求数列{bn}的前n项和Sn.
参考答案：
【答案】见解析
【解析】解 (1)设数列{an}的公差为d，
由已知，得
解得
故an＝3－(n－1)＝4－n.
(2)由(1)可得bn＝n·qn－1，
于是Sn＝1·q0＋2·q1＋3·q2＋…＋n·qn－1.
若q≠1，将上式两边同时乘以q，得
qSn＝1·q1＋2·q2＋…＋(n－1)·qn－1＋n·qn.
两式相减，得(q－1)Sn＝nqn－1－q1－q2－…－qn－1
＝nqn－
＝
.
于是，Sn＝
.
若q＝1，则Sn＝1＋2＋3＋…＋n＝
.
综上，Sn＝
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC中，内角A，B，C所对的边分别为a，b，c，且满足asinA-csinC=b(sinA－sinB）．
（Ⅰ）求角C的大小；
（Ⅱ）若边长c=4，求△ABC的周长最大值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】设f(x)是R上的偶函数，且在[0,+∞)上单调递增，则f(-2),f(3),f(-
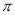)的大小顺序是：（ ）A. f(-
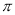)>f(3)>f(-2) B. f(-
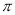) >f(-2)>f(3)C. f(-2)>f(3)> f(-
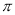) D. f(3)>f(-2)> f(-
) -
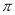科目： 来源： 题型：
查看答案和解析>>【题目】本着健康、低碳的生活理念，租用公共自行车的人越来越多.租用公共自行车的收费标准是每车每次不超过两小时免费，超过两小时的部分每小时2元（不足1小时的部分按1小时计算）.甲乙两人相互独立租车（各租一车一次）.设甲、乙不超过两小时还车的概率分别为
， 
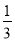；两小时以上且不超过三小时还车的概率分别为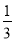
， 
；两人租车时间都不会超过四小时.（1）求出甲、乙所付租车费用相同的概率；
（2）设甲、乙两人所付的租车费用之和为随机变量
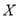，求随机变量
的概率分布和期望. -
科目： 来源： 题型：
查看答案和解析>>【题目】设函数
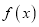是定义在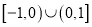
上的偶函数，当
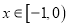时， 
）.（1）当
时，求
的解析式；（2）若
，试判断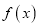
的上单调性，并证明你的结论；（3）是否存在
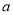，使得当
时， 
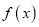有最大值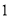
. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f(x)＝x3－3ax－1，a≠0.
(1)求f(x)的单调区间；
(2)若f(x)在x＝－1处取得极值，直线y＝m与y＝f(x)的图象有三个不同的交点，求m的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知等差数列{an}中公差d≠0，有a1+a4=14，且a1，a2，a7成等比数列．
（Ⅰ）求{an}的通项公式an与前n项和公式Sn；
（Ⅱ）令bn=
(k<0)，若{bn}是等差数列，求数列{
}的前n项和Tn．
相关试题
