【题目】设函数![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)当![]() 时,
时, ![]() .
.
参考答案:
【答案】(Ⅰ) 见解析;(Ⅱ) 见解析.
【解析】试题分析:(Ⅰ) 求导得![]() ,分
,分![]() ,
, ![]() ,
, ![]() 三种情况讨论可得
三种情况讨论可得![]() 的单调区间.
的单调区间.
(Ⅱ)当![]() 时,
时, ![]() 和
和![]() 可得所有的
可得所有的![]() ,
, ![]() ;
;
当![]() 时,易知
时,易知![]() 上均有
上均有![]() .
.
只需考虑![]() 时,此时
时,此时![]() ,分
,分![]() 和
和![]() 两种情况讨论即可.
两种情况讨论即可.
试题解析:(Ⅰ) ![]() .
.
①当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() .当
.当![]() 时,
时, ![]() .∴
.∴![]() 在
在![]() 递增
递增
②当![]() 时,令
时,令![]() ,得
,得![]() ,此时
,此时![]() .
.
易知![]() 在
在![]() 递增,
递增, ![]() 递减,
递减, ![]() 递增
递增
③当![]() 时,
时, ![]() .易知
.易知![]() 在
在![]() 递增,
递增, ![]() 递减,
递减, ![]() 递增
递增
(Ⅱ)当![]() 时,
时, ![]() ,
,
①若![]() 时,可知
时,可知![]() ,
,
②若![]() 时,由(Ⅰ)知
时,由(Ⅰ)知![]() 在
在![]() 上单调递增,则有
上单调递增,则有![]()
因此,当![]() 时,对所有的
时,对所有的![]() ,
, ![]() ;
;
当![]() 时,由(Ⅰ)可知易知
时,由(Ⅰ)可知易知![]() 在
在![]() 递增,
递增, ![]() 递减,
递减, ![]() 递增,
递增,
且![]() ,因此在
,因此在![]() 上均有
上均有![]() .
.
下面考虑![]() 时,此时
时,此时![]()
![]() ,其中,
,其中, ![]()
![]() .
.
设![]() ,则
,则![]()
①若![]() ,则
,则![]() ,
, ![]() ,而
,而![]()
∴![]() ,∴
,∴![]() ,即
,即![]() .
.
此时![]() 在
在![]() 递增,故
递增,故![]() ;
;
②若![]() ,则
,则![]()
由①②可知,二次函数![]() .
.
因此在![]() 时,总有
时,总有![]() .
.
综上,当![]() 时,对所有的
时,对所有的![]() ,
, ![]() .
.
点晴:本题主要考查函数单调性,不等式恒成立证明问题.要求单调性,求导比较导方程的根的大小,解不等式可得单调区间,要证明不等式恒成立问题,我们可以先根据题意构造新函数,求其值最值即可.这类问题的通解方法就是:划归与转化之后,就可以假设相对应的函数,然后利用导数研究这个函数的单调性、极值和最值,图像与性质,进而求解得结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若动点
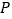 在直线
在直线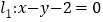 上,动点
上,动点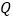 在直线
在直线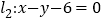 上,设线段
上,设线段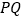 的中点为
的中点为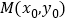 ,且
,且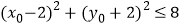 ,则
,则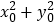 的取值范围是__________.
的取值范围是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2sin2(
 +x)﹣
+x)﹣ 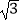 cos2x,
cos2x,
(1)求f(x)的最小正周期及单调递减区间;
(2)当x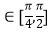 时,求f(x)的最大值和最小值.
时,求f(x)的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知四棱锥P﹣ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,求证:
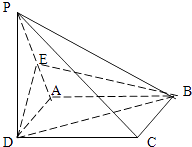
(1)PC∥平面EBD.
(2)平面PBC⊥平面PCD. -
科目: 来源: 题型:
查看答案和解析>>【题目】对某地区儿童的身高与体重的一组数据,我们用两种模型①
 ,②
,②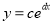 拟合,得到回归方程分别为
拟合,得到回归方程分别为 ,
, 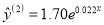 ,作残差分析,如表:
,作残差分析,如表:身高
60
70
80
90
100
110
体重
6
8
10
14
15
18
0.41
0.01
1.21
-0.19
0.41
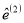
-0.36
0.07
0.12
1.69
-0.34
-1.12
(Ⅰ)求表中空格内的值;
(Ⅱ)根据残差比较模型①,②的拟合效果,决定选择哪个模型;
(Ⅲ)残差大于
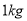 的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.(结果保留到小数点后两位)
附:对于一组数据
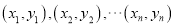 ,其回归直线
,其回归直线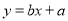 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为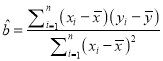 ,
, 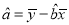 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点A(0,3),直线l:y=2x﹣4.设圆C的半径为1,圆心在l上.
(1)若圆心C也在直线y=﹣x+5上,求圆C的方程;
(2)在(1)的条件下,过点A作圆C的切线,求切线的方程;
(3)若圆C上存在点M,使|MA|=|MO|,求圆心C的横坐标a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=ax2+bx+c.
(1)若f(﹣1)=0,f(0)=0,求出函数f(x)的零点;
(2)若f(x)同时满足下列条件:①当x=﹣1时,函数f(x)有最小值0,②f(1)=1求函数f(x)的解析式;
(3)若f(1)≠f(3),证明方程f(x)= [f(1)+f(3)]必有一个实数根属于区间(1,3)
[f(1)+f(3)]必有一个实数根属于区间(1,3)
相关试题

