【题目】若数列{an}前n项和为Sn , a1=a2=2,且满足Sn+Sn+1+Sn+2=3n2+6n+5,则S47等于 .
参考答案:
【答案】2209
【解析】解:由Sn+Sn+1+Sn+2=3n2+6n+5可得Sn﹣1+Sn+Sn+1=3(n﹣1)2+6(n﹣1)+5,
两式相减可得an+an+1+an+2=6n+3,
∴数列{an+an+1+an+2}是公差为18的等差数列,
令n=3可得a3+a4+a5=21,
∴S47=a1+a2+(a3+a4+a5)+…+(a45+a46+a47)
=4+15×21+ ![]() ×18=2209,
×18=2209,
所以答案是:2209.
【考点精析】本题主要考查了等差数列的性质的相关知识点,需要掌握在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin(2x+φ),其中φ为实数,若f(x)≤|f(
 )|对x∈R恒成立,且f(
)|对x∈R恒成立,且f(  )>f(π),则f(x)的单调递增区间是( )
)>f(π),则f(x)的单调递增区间是( )
A.[kπ﹣ ,kπ+
,kπ+  ](k∈Z)
](k∈Z)
B.[kπ,kπ+ ](k∈Z)
](k∈Z)
C.[kπ+ ,kπ+
,kπ+  ](k∈Z)
](k∈Z)
D.[kπ﹣ ,kπ](k∈Z)
,kπ](k∈Z) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)若函数
 在其定义域上为单调增函数,求
在其定义域上为单调增函数,求 的取值范围;
的取值范围;(2)记
 的导函数为
的导函数为 ,当
,当 时,证明:
时,证明: 存在极小值点
存在极小值点 ,且
,且 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在(0,+∞)上的连续函数y=f(x)满足:xf′(x)﹣f(x)=xex且f(1)=﹣3,f(2)=0.则函数y=f(x)( )
A.有极小值,无极大值
B.有极大值,无极小值
C.既有极小值又有极大值
D.既无极小值又无极大值 -
科目: 来源: 题型:
查看答案和解析>>【题目】若数列{an}前n项和为Sn , a1=a2=2,且满足Sn+Sn+1+Sn+2=3n2+6n+5,则S47等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为选拔参加“央视猜灯谜大赛”的队员,在校内组织猜灯谜竞赛.规定:第一阶段知识测试成绩不小于160分的学生进入第二阶段比赛.现有200名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
(Ⅰ)估算这200名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
(Ⅱ)将进入第二阶段的学生分成若干队进行比赛.现甲、乙两队在比赛中均已获得120分,进入最后抢答阶段.抢答规则:抢到的队每次需猜3条谜语,猜对1条得20分,猜错1条扣20分.根据经验,甲队猜对每条谜语的概率均为 ,乙队猜对前两条的概率均为
,乙队猜对前两条的概率均为  ,猜对第3条的概率为
,猜对第3条的概率为  .若这两队抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
.若这两队抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,角
中,角 ,
, ,
,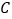 所对的边分别为
所对的边分别为 ,
,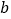 ,
, ,且
,且 ,则下列结论正确的是( )
,则下列结论正确的是( )A.
 B.
B. 是钝角三角形
是钝角三角形C.
 的最大内角是最小内角的
的最大内角是最小内角的 倍D.若
倍D.若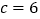 ,则
,则 外接圆半径为
外接圆半径为
相关试题

