【题目】点P是椭圆 ![]() 上的一点,F1和F2是焦点,且
上的一点,F1和F2是焦点,且 ![]() ,则△F1PF2的周长为 , △F1PF2的面积为 .
,则△F1PF2的周长为 , △F1PF2的面积为 .
参考答案:
【答案】6;![]()
【解析】解:由椭圆 ![]() ,a=2,b=
,a=2,b= ![]() ,c=1, 由椭圆的定义可知:|PF1|+|PF2|=2a=4,
,c=1, 由椭圆的定义可知:|PF1|+|PF2|=2a=4,
△F1PF2的周长为|PF1|+|PF2|+|F1F2|=2a+2c=6,
∴△F1PF2的周长为6,
方法一:将|PF1|+|PF2|=2a=4,两边平方,得|PF1|2+|PF2|2+2|PF1||PF2|=16,(1)
在△F1PF2中,由|F1F2|=2c,∠F1PF2=60°,
由余弦定理,得|PF1|2+|PF2|2+2|PF1||PF2|cos60°=|F1F2|2=4
即|PF1|2+|PF2|2+2|PF1||PF2|=4,(2)
·(1)﹣(2),得:3|PF1||PF2|=12,
∴|PF1||PF2|=4.
∴△F1PF2的面积S= ![]() |PF1||PF2|sin60°=
|PF1||PF2|sin60°= ![]() ×4×
×4× ![]() =
= ![]() ,
,
方法二:设∠F1PF2=θ,由焦点三角形的面积公式可知:S=b2 ![]() =b2tan
=b2tan ![]() =3×tan30°=3×
=3×tan30°=3× ![]() =
= ![]() ,
,
所以答案是:6, ![]() ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意实数a,b,c,d,以下四个命题中的真命题是( )
A.若a>b,c≠0则ac>bc
B.若a>b>o,c>d则ac>bd
C.若a>b,则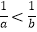
D.若ac2>bc2则a>b -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 (
( )离心率为
)离心率为 ,过点
,过点 的椭圆的两条切线相互垂直.
的椭圆的两条切线相互垂直.(1)求此椭圆的方程;
(2)若存在过点
 的直线
的直线 交椭圆于
交椭圆于 两点,使得
两点,使得 (
( 为右焦点),求
为右焦点),求 的范围.
的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  是
是 的导函数.
的导函数.(1)若
 在
在 处的切线方程为
处的切线方程为 ,求
,求 的值;
的值;(2)若
 且
且 在
在 时取得最小值,求
时取得最小值,求 的取值范围;
的取值范围;(3)在(1)的条件下,当
 时,
时,  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体ABCD﹣A1B1C1D1中,E,F,G分别为A1B1 , BB1 , B1C1的中点,则AC1与D1E所成角的余弦值为 , AC1与平面EFG所成角的正弦值为 .
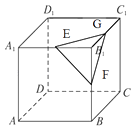
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知F1 , F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A,B两点,若△ABF2是正三角形,则这个椭圆的离心率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组函数中不表示同一函数的是( )
A.f(x)=lgx2 , g(x)=2lg|x|
B.f(x)=x,g(x)=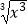
C.f(x)=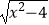 ,g(x)=
,g(x)= 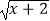
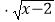
D.f(x)=|x+1|,g(x)=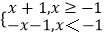
相关试题

