【题目】下列各组函数中不表示同一函数的是( )
A.f(x)=lgx2 , g(x)=2lg|x|
B.f(x)=x,g(x)= ![]()
C.f(x)= ![]() ,g(x)=
,g(x)= ![]()
![]()
D.f(x)=|x+1|,g(x)= ![]()
参考答案:
【答案】C
【解析】解:对于A:f(x)=lgx2=2lg|x|的定义域为{x|x≠0},g(x)=2lg|x|的定义域为{x|x≠0},定义域相同,对应关系也相同,∴是同一函数;
对于B:f(x)=x的定义域为R,g(x)= ![]() =x的定义域为R,定义域相同,对应关系也相同,∴是同一函数;
=x的定义域为R,定义域相同,对应关系也相同,∴是同一函数;
对于C:f(x)= ![]() 的定义域为{x|x≥2或x≤﹣2},而g(x)=
的定义域为{x|x≥2或x≤﹣2},而g(x)= ![]()
![]() 的定义域为{x|x≥2},定义域不同,∴不是同一函数;
的定义域为{x|x≥2},定义域不同,∴不是同一函数;
对于D:f(x)=|x+1|= ![]() 的定义域为R,g(x)=
的定义域为R,g(x)= ![]() 的定义域为R,对应关系也相同,∴是同一函数;
的定义域为R,对应关系也相同,∴是同一函数;
故选:C.
【考点精析】解答此题的关键在于理解判断两个函数是否为同一函数的相关知识,掌握只有定义域和对应法则二者完全相同的函数才是同一函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P是椭圆
 上的一点,F1和F2是焦点,且
上的一点,F1和F2是焦点,且  ,则△F1PF2的周长为 , △F1PF2的面积为 .
,则△F1PF2的周长为 , △F1PF2的面积为 . -
科目: 来源: 题型:
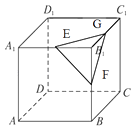
查看答案和解析>>【题目】在正方体ABCD﹣A1B1C1D1中,E,F,G分别为A1B1 , BB1 , B1C1的中点,则AC1与D1E所成角的余弦值为 , AC1与平面EFG所成角的正弦值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知F1 , F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A,B两点,若△ABF2是正三角形,则这个椭圆的离心率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆的两个焦点为
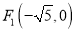 ,
, 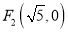 是椭圆上一点,若
是椭圆上一点,若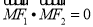 ,
, 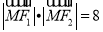 .
.(1)求椭圆的方程;
(2)直线
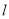 过右焦点
过右焦点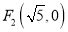 (不与
(不与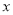 轴重合)且与椭圆相交于不同的两点
轴重合)且与椭圆相交于不同的两点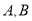 ,在
,在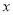 轴上是否存在一个定点
轴上是否存在一个定点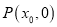 ,使得
,使得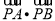 的值为定值?若存在,写出
的值为定值?若存在,写出 点的坐标(不必求出定值);若不存在,说明理由.
点的坐标(不必求出定值);若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】有下列五个命题: ①平面内,到一定点的距离等于到一定直线距离的点的集合是抛物线;
②平面内,定点F1、F2 , |F1F2|=6,动点M满足|MF1|+|MF2|=6,则点M的轨迹是椭圆;
③在△ABC中,“∠B=60°”是“∠A,∠B,∠C三个角成等差数列”的充要条件;
④“若﹣3<m<5,则方程 =1是椭圆”.
=1是椭圆”.
⑤已知向量 ,
,  ,
,  是空间的一个基底,则向量
是空间的一个基底,则向量  +
+  ,
,  ﹣
﹣  ,
,  也是空间的一个基底.
也是空间的一个基底.
其中真命题的序号是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)的定义域为(﹣1,1),则函数g(x)=f(
 )+f(x﹣1)的定义域为( )
)+f(x﹣1)的定义域为( )
A.(﹣2,0)
B.(﹣2,2)
C.(0,2)
D.(﹣ ,0)
,0)
相关试题

