【题目】如图,在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,且过点(1,
,且过点(1,![]() ).过椭圆C的左顶点A作直线交椭圆C于另一点P,交直线l:x=m(m>a)于点M.已知点B(1,0),直线PB交l于点N.
).过椭圆C的左顶点A作直线交椭圆C于另一点P,交直线l:x=m(m>a)于点M.已知点B(1,0),直线PB交l于点N.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若MB是线段PN的垂直平分线,求实数m的值.

参考答案:
【答案】(1)![]() +y2=1(2)
+y2=1(2)![]()
【解析】试题分析:(1)根据题意列出关于![]() 、
、![]() 、
、![]() 的方程组,结合性质
的方程组,结合性质![]() ,
,![]() ,求出
,求出![]() 、
、![]() 、
、![]() ,即可得结果;(2)设
,即可得结果;(2)设![]() ,则
,则![]() ,所以
,所以![]() .可得直线
.可得直线![]() 的方程为
的方程为![]() ,根据
,根据![]() 可得
可得![]() ,解方程即可得结果.
,解方程即可得结果.
试题解析:(1)因为椭圆C的离心率为![]() ,所以a2=4b2.
,所以a2=4b2.
又因为椭圆C过点(1,![]() ),所以
),所以![]() +
+![]() =1,
=1,
解得a2=4,b2=1.
所以椭圆C的方程为![]() +y2=1.
+y2=1.
(2)解法1
设P(x0,y0),-2<x0<2, x0≠1,则![]() +y02=1.
+y02=1.
因为MB是PN的垂直平分线,所以P关于B的对称点N(2-x0,-y0),
所以2-x0=m.
由A(-2,0),P(x0,y0),可得直线AP的方程为y=![]() (x+2),
(x+2),
令x=m,得y=![]() ,即M(m,
,即M(m,![]() ).
).
因为PB⊥MB,所以kPB·kMB=-1,
所以kPB·kMB=![]() ·
·![]() =-1,
=-1,
即![]() =-1.
=-1.
因为![]() +y02=1.所以
+y02=1.所以![]() =1.
=1.
因为x0=2-m ,所以化简得3m2-10m+4=0,
解得m=![]() .
.
因为m>2,所以m=![]() .
.
解法2
①当AP的斜率不存在或为0时,不满足条件.
②设AP斜率为k,则AP:y=k(x+2),
联立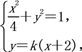 消去y得(4k2+1)x2+16k2x+16k2-4=0.
消去y得(4k2+1)x2+16k2x+16k2-4=0.
因为xA=-2,所以xP=![]() ,所以yP=
,所以yP=![]() ,
,
所以P(![]() ,
,![]() ).
).
因为PN的中点为B,所以m=2-![]() =
=![]() .(*)
.(*)
因为AP交直线l于点M,所以M(m,k(m+2)),
因为直线PB与x轴不垂直,所以![]() ≠1,即k2≠
≠1,即k2≠![]() ,
,
所以kPB= =
=![]() ,kMB=
,kMB=![]() .
.
因为PB⊥MB,所以kPB·kMB=-1,
所以![]() ·
·![]() =-1.(**)
=-1.(**)
将(*)代入(**),化简得48k4-32k2+1=0,
解得k2=![]() ,所以m=
,所以m=![]() =
=![]() .
.
又因为m>2,所以m=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AP=AB=AD=1.
(Ⅰ)若直线PB与CD所成角的大小为
 ,求BC的长;
,求BC的长;(Ⅱ)求二面角B-PD-A的余弦值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
已知数列{an}的各项均为正数,记数列{an}的前n项和为Sn,数列{an2}的前n项和为Tn,且3Tn=Sn2+2Sn,n∈N*.
(Ⅰ)求a1的值;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)若k,t∈N*,且S1,Sk-S1,St-Sk成等比数列,求k和t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x+
 (x>0,m>0)和函数g(x)=a|x﹣b|+c(x∈R,a>0,b>0).问:
(x>0,m>0)和函数g(x)=a|x﹣b|+c(x∈R,a>0,b>0).问:
(1)证明:f(x)在(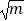 ,+∞)上是增函数;
,+∞)上是增函数;
(2)把函数g1(x)=|x|和g2(x)=|x﹣1|写成分段函数的形式,并画出它们的图象,总结出g2(x)的图象是如何由g1(x)的图象得到的.请利用上面你的结论说明:g(x)的图象关于x=b对称;
(3)当m=1,b=2,c=0时,若f(x)>g(x)对于任意的x>0恒成立,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】
某工厂有100名工人接受了生产1000台某产品的总任务,每台产品由9个甲型装置和3个乙型装置配套组成,每个工人每小时能加工完成1个甲型装置或3个乙型装置.现将工人分成两组分别加工甲型和乙型装置.设加工甲型装置的工人有x人,他们加工完甲型装置所需时间为t1小时,其余工人加工完乙型装置所需时间为t2小时.
设f(x)=t1+t2.
(Ⅰ)求f(x)的解析式,并写出其定义域;
(Ⅱ)当x等于多少时,f(x)取得最小值?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四组函数中,表示相等函数的一组是( )
A.f(x)=|x|,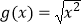
B.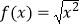 ,
, 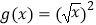
C.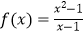 ,g(x)=x+1
,g(x)=x+1
D.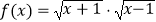 ,
, 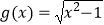
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
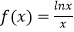
(1)求函数f(x)的单调区间;
(2)设a>0,求函数f(x)在[2a,4a]上的最小值;
(3)某同学发现:总存在正实数a、b(a<b),使ab=ba , 试问:他的判断是否正确?若不正确,请说明理由;若正确,请直接写出a的取值范围(不需要解答过程).
相关试题

