【题目】
已知数列{an}的各项均为正数,记数列{an}的前n项和为Sn,数列{an2}的前n项和为Tn,且3Tn=Sn2+2Sn,n∈N*.
(Ⅰ)求a1的值;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)若k,t∈N*,且S1,Sk-S1,St-Sk成等比数列,求k和t的值.
参考答案:
【答案】(1)1(2)an=2n-1,n∈N*(3) k=2,t=3
【解析】试题分析:(1)由![]() ,得
,得![]() ,解方程即可得结果;(2)因为
,解方程即可得结果;(2)因为![]() ,两式相减可得
,两式相减可得![]() 再得
再得![]() ,再相减可得
,再相减可得![]() 是等差数列,从而可得结果;(3)由(2)可知
是等差数列,从而可得结果;(3)由(2)可知![]() ,根据
,根据![]() 成等比数列可得
成等比数列可得![]() ,只需证明以上等式无整数解即可.
,只需证明以上等式无整数解即可.
试题解析:(1)由3T1=S12+2S1,得3a12=a12+2a1,即a12-a1=0.
因为a1>0,所以a1=1.
(2)因为3Tn=Sn2+2Sn, ①
所以3Tn+1=Sn+12+2Sn+1,②
②-①,得3an+12=Sn+12-Sn2+2an+1.
因为an+1>0,
所以3an+1=Sn+1+Sn+2, ③
所以3an+2=Sn+2+Sn+1+2,④
④-③,得3an+2-3an+1=an+2+an+1,即an+2=2an+1,
所以当n≥2时,![]() =2.
=2.
又由3T2=S22+2S2,得3(1+a22)=(1+a2)2+2(1+a2),
即a22-2a2=0.
因为a2>0,所以a2=2,所以![]() =2,所以对n∈N*,都有
=2,所以对n∈N*,都有![]() =2成立,
=2成立,
所以数列{an}的通项公式为an=2n-1,n∈N*.
(3)由(2)可知Sn=2n-1.
因为S1,Sk-S1,St-Sk成等比数列,
所以(Sk-S1)2=S1(St-Sk),即(2k-2)2=2t-2k,
所以2t=(2k)2-32k+4,即2t-2=(2k-1)2-32k-2+1(*).
由于Sk-S1≠0,所以k≠1,即k≥2.
当k=2时,2t=8,得t=3.
当k≥3时,由(*),得(2k-1)2-32k-2+1为奇数,
所以t-2=0,即t=2,代入(*)得22k-2-32k-2=0,即2k=3,此时k无正整数解.
综上,k=2,t=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
袋中有形状和大小完全相同的四种不同颜色的小球,每种颜色的小球各有4个,分别编号为1,2,3,4.现从袋中随机取两个球.
(Ⅰ)若两个球颜色不同,求不同取法的种数;
(Ⅱ)在(1)的条件下,记两球编号的差的绝对值为随机变量X,求随机变量X的概率分布与数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在半径为3m的
 圆形(O为圆心)铝皮上截取一块矩形材料OABC,其中点B在圆弧上,点A、C在两半径上,现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长AB=xm,圆柱的体积为Vm3 .
圆形(O为圆心)铝皮上截取一块矩形材料OABC,其中点B在圆弧上,点A、C在两半径上,现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长AB=xm,圆柱的体积为Vm3 . 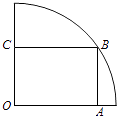
(1)写出体积V关于x的函数关系式,并指出定义域;
(2)当x为何值时,才能使做出的圆柱形罐子体积V最大?最大体积是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AP=AB=AD=1.
(Ⅰ)若直线PB与CD所成角的大小为
 ,求BC的长;
,求BC的长;(Ⅱ)求二面角B-PD-A的余弦值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x+
 (x>0,m>0)和函数g(x)=a|x﹣b|+c(x∈R,a>0,b>0).问:
(x>0,m>0)和函数g(x)=a|x﹣b|+c(x∈R,a>0,b>0).问:
(1)证明:f(x)在(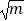 ,+∞)上是增函数;
,+∞)上是增函数;
(2)把函数g1(x)=|x|和g2(x)=|x﹣1|写成分段函数的形式,并画出它们的图象,总结出g2(x)的图象是如何由g1(x)的图象得到的.请利用上面你的结论说明:g(x)的图象关于x=b对称;
(3)当m=1,b=2,c=0时,若f(x)>g(x)对于任意的x>0恒成立,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,椭圆C:
 (a>b>0)的离心率为
(a>b>0)的离心率为 ,且过点(1,
,且过点(1, ).过椭圆C的左顶点A作直线交椭圆C于另一点P,交直线l:x=m(m>a)于点M.已知点B(1,0),直线PB交l于点N.
).过椭圆C的左顶点A作直线交椭圆C于另一点P,交直线l:x=m(m>a)于点M.已知点B(1,0),直线PB交l于点N.(Ⅰ)求椭圆C的方程;
(Ⅱ)若MB是线段PN的垂直平分线,求实数m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
某工厂有100名工人接受了生产1000台某产品的总任务,每台产品由9个甲型装置和3个乙型装置配套组成,每个工人每小时能加工完成1个甲型装置或3个乙型装置.现将工人分成两组分别加工甲型和乙型装置.设加工甲型装置的工人有x人,他们加工完甲型装置所需时间为t1小时,其余工人加工完乙型装置所需时间为t2小时.
设f(x)=t1+t2.
(Ⅰ)求f(x)的解析式,并写出其定义域;
(Ⅱ)当x等于多少时,f(x)取得最小值?
相关试题

