【题目】已知函数![]() .
.
(1)求![]() 的最大值;
的最大值;
(2)当![]() 时,函数
时,函数![]() 有最小值. 记
有最小值. 记![]() 的最小值为
的最小值为![]() ,求函数
,求函数![]() 的值域.
的值域.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)首先求得导函数,然后根据导函数与0的关系求得函数![]() 的单调区间,从而求得
的单调区间,从而求得![]() 的最大值;(2)首先求得
的最大值;(2)首先求得![]() ,然后结合(1)分
,然后结合(1)分![]() 、
、![]() 求得函数的单调区间与最小值的函数解析式,再通过求导研究其的单调性,从而求得
求得函数的单调区间与最小值的函数解析式,再通过求导研究其的单调性,从而求得![]() 的值域.
的值域.
试题解析:(1)f′(x)=(x>0),
当x∈(0,e)时,f′(x)>0,f(x)单调递增;
当x∈(e,+∞)时,f′(x)<0,f(x)单调递减,
所以当x=e时,f(x)取得最大值f(e)=. …4分
(2)g′(x)=lnx-ax=x(-a),由(1)及x∈(0,e]得:
①当a=时,-a≤0,g′(x)≤0,g(x)单调递减,
当x=e时,g(x)取得最小值g(e)=h(a)=-. …6分
②当a∈[0,),f(1)=0≤a,f(e)=>a,
所以存在t∈[1,e),g′(t)=0且lnt=at,
当x∈(0,t)时,g′(x)<0,g(x)单调递减,当x∈(t,e]时,g′(x)>0,g(x)单调递增,
所以g(x)的最小值为g(t)=h(a). …9分
令h(a)=G(t)=-t,
因为G′(t)=<0,所以G(t)在[1,e)单调递减,此时G(t)∈(-,-1].
综上,h(a)∈[-,-1]. …12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
 中,底面
中,底面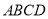 是边长为
是边长为 的菱形,
的菱形, ,
, .
.
(1)证明:
 平面
平面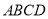 ;
;(2)若
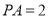 ,求二面角
,求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】有两枚均匀的硬币和一枚不均匀的硬币,其中不均匀的硬币抛掷后出现正面的概率为
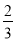 ,小华先抛掷这三枚硬币,然后小红再抛掷这三枚硬币.
,小华先抛掷这三枚硬币,然后小红再抛掷这三枚硬币.(1)求小华抛得一个正面两个反面且小红抛得两个正面一个反面的概率;
(2)若用
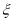 表示小华抛得正面的个数,求
表示小华抛得正面的个数,求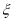 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,曲线
中,曲线 ,曲线
,曲线 为参数), 以坐标原点
为参数), 以坐标原点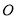 为极点,
为极点,  轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.(1)求曲线
 的极坐标方程;
的极坐标方程;(2)若射线
 分别交
分别交 于
于 两点, 求
两点, 求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
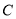 :
: 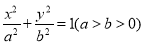 ,圆
,圆 :
: 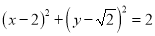 的圆心
的圆心 在椭圆上,点
在椭圆上,点 到椭圆
到椭圆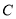 的右焦点的距离为
的右焦点的距离为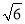 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)过点
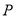 作互相垂直的两条直线
作互相垂直的两条直线 ,且
,且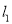 交椭圆
交椭圆 于
于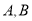 两点,直线
两点,直线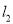 交圆
交圆 于
于 ,
, 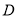 两点,且
两点,且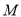 为
为 的中点,求
的中点,求 面积的取值范围.
面积的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,角
中,角 、
、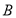 、
、 所对的边分别为
所对的边分别为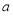 、
、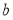 、
、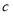 .已知
.已知 .
.(1)求
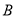 ;
;(2)若
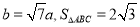 ,求
,求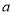 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的几何体中,四边形
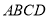 是菱形,
是菱形, 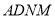 是矩形,平面
是矩形,平面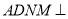 平面
平面 ,
, 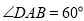 ,
, 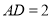 ,
,  ,
, 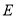 为
为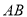 的中点.
的中点.(1)求证:
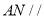 平面
平面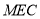 ;
;(2)在线段
 上是否存在点
上是否存在点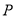 ,使二面角
,使二面角 的大小为
的大小为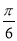 ?若存在,求出
?若存在,求出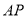 的长
的长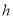 ,若不存在,请说明理由.
,若不存在,请说明理由.
相关试题

