【题目】已知椭圆![]() :
: ![]() ,圆
,圆![]() :
: ![]() 的圆心
的圆心![]() 在椭圆上,点
在椭圆上,点![]() 到椭圆
到椭圆![]() 的右焦点的距离为
的右焦点的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() ,且
,且![]() 交椭圆
交椭圆![]() 于
于![]() 两点,直线
两点,直线![]() 交圆
交圆![]() 于
于![]() ,
, ![]() 两点,且
两点,且![]() 为
为![]() 的中点,求
的中点,求![]() 面积的取值范围.
面积的取值范围.

参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)求椭圆标准方程,一般方法为待定系数法,只需列出两个独立条件,解方程组即可:一是圆心![]() 在椭圆上,即
在椭圆上,即![]() ,二是根据两点间距离公式得
,二是根据两点间距离公式得![]() ,解得
,解得![]() ,
, ![]() ,(2)设直线
,(2)设直线![]() :
: ![]() ,直线
,直线![]() 的方程为
的方程为![]() ,根据几何条件得
,根据几何条件得![]() ,所以△
,所以△![]() 的面积等于
的面积等于![]() ,先根据点到直线距离公式得
,先根据点到直线距离公式得![]() ,再联立直线方程与椭圆方程,结合韦达定理、弦长公式得
,再联立直线方程与椭圆方程,结合韦达定理、弦长公式得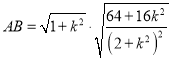 ,即
,即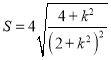 ,最后根据分式函数值域求法得范围
,最后根据分式函数值域求法得范围
试题解析:(1)圆![]() :
: ![]() 的圆心为
的圆心为![]() ,
,
代入椭圆方程可得![]() ,
,
由点![]() 到椭圆
到椭圆![]() 的右焦点的距离为
的右焦点的距离为![]() ,即有
,即有![]() ,
,
解得![]() ,即
,即![]() ,
,
解得![]() ,
, ![]() ,
,
即有椭圆方程为![]() .
.
(2)依题意知直线![]() 斜率必存在,当斜率为0时,直线
斜率必存在,当斜率为0时,直线![]() :
: ![]() ,
,
代入圆的方程可得![]() ,可得
,可得![]() 的坐标为
的坐标为![]() ,又
,又![]() ,
,
可得![]() 的面积为
的面积为![]() ;
;
当直线![]() 斜率不为0时设直线
斜率不为0时设直线![]() :
: ![]() ,代入圆
,代入圆![]() 的方程可得
的方程可得
![]() ,
,
可得中点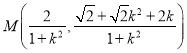 ,
,
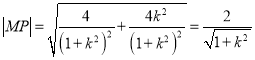 ,
,
此时直线![]() 的方程为
的方程为![]() ,代入椭圆方程,可得:
,代入椭圆方程,可得:
![]() ,
,
设![]() ,
, ![]() ,可得
,可得![]() ,
, ![]() ,
,
则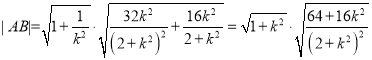 ,
,
可得![]() 的面积为
的面积为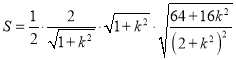
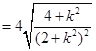 ,
,
设![]() (
(![]() ),可得
),可得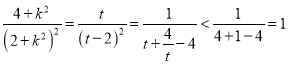 ,
,
可得![]() ,且
,且![]() ,
,
综上可得,△![]() 的面积的取值范围是
的面积的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两枚均匀的硬币和一枚不均匀的硬币,其中不均匀的硬币抛掷后出现正面的概率为
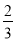 ,小华先抛掷这三枚硬币,然后小红再抛掷这三枚硬币.
,小华先抛掷这三枚硬币,然后小红再抛掷这三枚硬币.(1)求小华抛得一个正面两个反面且小红抛得两个正面一个反面的概率;
(2)若用
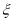 表示小华抛得正面的个数,求
表示小华抛得正面的个数,求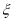 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,曲线
中,曲线 ,曲线
,曲线 为参数), 以坐标原点
为参数), 以坐标原点 为极点,
为极点,  轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.(1)求曲线
 的极坐标方程;
的极坐标方程;(2)若射线
 分别交
分别交 于
于 两点, 求
两点, 求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求
 的最大值;
的最大值;(2)当
 时,函数
时,函数 有最小值. 记
有最小值. 记 的最小值为
的最小值为 ,求函数
,求函数 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,角
中,角 、
、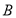 、
、 所对的边分别为
所对的边分别为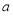 、
、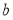 、
、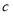 .已知
.已知 .
.(1)求
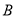 ;
;(2)若
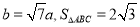 ,求
,求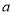 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的几何体中,四边形
 是菱形,
是菱形, 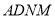 是矩形,平面
是矩形,平面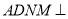 平面
平面 ,
, 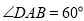 ,
, 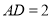 ,
,  ,
, 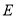 为
为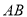 的中点.
的中点.(1)求证:
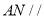 平面
平面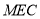 ;
;(2)在线段
 上是否存在点
上是否存在点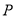 ,使二面角
,使二面角 的大小为
的大小为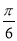 ?若存在,求出
?若存在,求出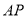 的长
的长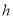 ,若不存在,请说明理由.
,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为
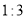 ,且成绩分布在
,且成绩分布在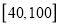 ,分数在
,分数在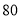 以上(含
以上(含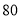 )的同学获奖. 按文理科用分层抽样的方法抽取
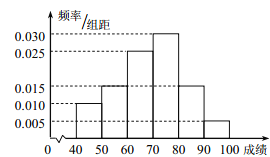
)的同学获奖. 按文理科用分层抽样的方法抽取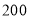 人的成绩作为样本,得到成绩的频率分布直方图(见下图).
人的成绩作为样本,得到成绩的频率分布直方图(见下图).(1)求
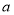 的值,并计算所抽取样本的平均值
的值,并计算所抽取样本的平均值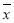 (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);(2)填写下面的
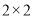 列联表,能否有超过
列联表,能否有超过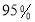 的把握认为“获奖与学生的文理科有关”?
的把握认为“获奖与学生的文理科有关”?文科生
理科生
合计
获奖
不获奖
合计
附表及公式:
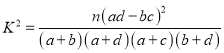 ,其中
,其中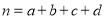
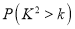
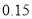
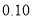
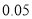
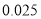
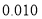
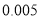
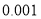
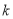
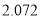


相关试题

