【题目】有两枚均匀的硬币和一枚不均匀的硬币,其中不均匀的硬币抛掷后出现正面的概率为![]() ,小华先抛掷这三枚硬币,然后小红再抛掷这三枚硬币.
,小华先抛掷这三枚硬币,然后小红再抛掷这三枚硬币.
(1)求小华抛得一个正面两个反面且小红抛得两个正面一个反面的概率;
(2)若用![]() 表示小华抛得正面的个数,求
表示小华抛得正面的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)设![]() 表示事件“小华抛得一个正面两个反面”,
表示事件“小华抛得一个正面两个反面”, ![]() 表示事件“小红抛得两个正面一个反面”,可得
表示事件“小红抛得两个正面一个反面”,可得![]() ,由独立事件的概率公式可得;(2)由题意
,由独立事件的概率公式可得;(2)由题意![]() 的取值范围为
的取值范围为![]() ,可求其概率,可得
,可求其概率,可得![]() 的分布列,进而可得数学期望.
的分布列,进而可得数学期望.
试题解析:解:(1)设![]() 表示事件“小华抛得一个正面两个反面”,
表示事件“小华抛得一个正面两个反面”, ![]() 表示事件“小红抛得两个正面一个反面”,
表示事件“小红抛得两个正面一个反面”,
则![]() ,
, ![]() ,
,
则小华抛得一个正面两个反面且小红抛得两个正面一个反面的概率为
![]() . “”
. “”
(2)由题意,![]() 的取值为0,1,2,3,且
的取值为0,1,2,3,且![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
所求随机变量![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
数学期望![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车公司为确定下一年度投入某种产品的宣传费,需了解年宣传费(单位:千元)对年利润
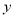 (单位:万元)的影响,对近5年的宣传费
(单位:万元)的影响,对近5年的宣传费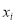 和年利润
和年利润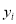 (
(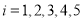 )进行了统计,列出了下表:
)进行了统计,列出了下表: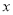 (单位:千元)
(单位:千元)2
4
7
17
30
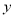 (单位:万元)
(单位:万元)1
2
3
4
5
员工小王和小李分别提供了不同的方案.
(1)小王准备用线性回归模型拟合
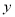 与
与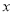 的关系,请你帮助建立
的关系,请你帮助建立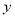 关于
关于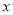 的线性回归方程;(系数精确到0.01)
的线性回归方程;(系数精确到0.01)(2)小李决定选择对数回归模型拟合
 与
与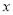 的关系,得到了回归方程:
的关系,得到了回归方程: 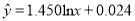 ,并提供了相关指数
,并提供了相关指数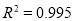 .请用相关指数说明哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析数据
.请用相关指数说明哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析数据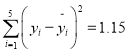 )
)参考公式:相关指数
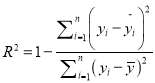
回归方程
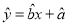 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: 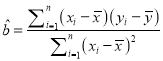 ,
, 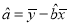 .参考数据:
.参考数据: 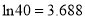 ,
, 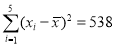 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  .
.(1)求函数
 在
在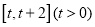 的最小值;
的最小值; (2)若函数
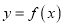 与
与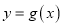 的图象恰有一个公共点,求实数
的图象恰有一个公共点,求实数 的值;
的值;(3)若函数
 有两个不同的极值点
有两个不同的极值点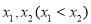 ,且
,且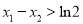 ,求实数
,求实数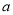 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
 中,底面
中,底面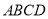 是边长为
是边长为 的菱形,
的菱形, ,
, .
.
(1)证明:
 平面
平面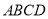 ;
;(2)若
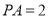 ,求二面角
,求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,曲线
中,曲线 ,曲线
,曲线 为参数), 以坐标原点
为参数), 以坐标原点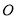 为极点,
为极点,  轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.(1)求曲线
 的极坐标方程;
的极坐标方程;(2)若射线
 分别交
分别交 于
于 两点, 求
两点, 求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求
 的最大值;
的最大值;(2)当
 时,函数
时,函数 有最小值. 记
有最小值. 记 的最小值为
的最小值为 ,求函数
,求函数 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
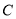 :
: 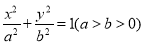 ,圆
,圆 :
: 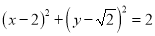 的圆心
的圆心 在椭圆上,点
在椭圆上,点 到椭圆
到椭圆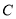 的右焦点的距离为
的右焦点的距离为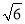 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)过点
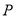 作互相垂直的两条直线
作互相垂直的两条直线 ,且
,且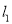 交椭圆
交椭圆 于
于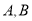 两点,直线
两点,直线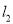 交圆
交圆 于
于 ,
, 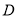 两点,且
两点,且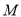 为
为 的中点,求
的中点,求 面积的取值范围.
面积的取值范围.
相关试题

