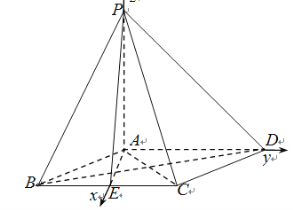
【题目】在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
,![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】
试题分析:(1)连接![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() ,然后根据等腰三角形的性质得出
,然后根据等腰三角形的性质得出![]() ,
,![]() ,从而推出
,从而推出![]() 平面
平面![]() ,进而利用线面垂直的性质定理结合判定定理可使问题得证;(2)以
,进而利用线面垂直的性质定理结合判定定理可使问题得证;(2)以![]() 为原点,建立空间直角坐标系,然后求得相关点的坐标与向量,由此求得平面
为原点,建立空间直角坐标系,然后求得相关点的坐标与向量,由此求得平面![]() 与平面
与平面![]() 的法向量,从而利用空间夹角公式求解.
的法向量,从而利用空间夹角公式求解.
试题解析:连接AC,则△ABC和△ACD都是正三角形,取BC中点E,连接AE,PE,
因为E为BC的中点,所以在△ABC中,![]() ,
,
因为PB=PC,所以BC⊥PE,
又因为PE∩AE=E,所以BC⊥平面PAE,
又PA平面PAE,所以BC⊥PA.
同理CD⊥PA,
又因为BC∩CD=C,所以PA⊥平面ABCD. …6
(2)如图,以A为原点,建立空间直角坐标系A-xyz,
则B(,-1,0),D(0,2,0),P(0,0,2),=(0,2,-2),=(-,3,0),
设平面PBD的法向量为m=(x,y,z),则即
取平面PBD的法向量m=(,1,1), …9分
取平面PAD的法向量n=(1,0,0),则cosm,n==,
所以二面角A-PD-B的余弦值是. …12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 为偶函数,且函数
为偶函数,且函数 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 .
.(1)求
 的值;
的值;(2)函数
 的图象向右平移
的图象向右平移 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数 的图象,求
的图象,求 的单调递减区间.
的单调递减区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车公司为确定下一年度投入某种产品的宣传费,需了解年宣传费(单位:千元)对年利润
 (单位:万元)的影响,对近5年的宣传费
(单位:万元)的影响,对近5年的宣传费 和年利润
和年利润 (
(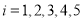 )进行了统计,列出了下表:
)进行了统计,列出了下表: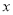 (单位:千元)
(单位:千元)2
4
7
17
30
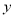 (单位:万元)
(单位:万元)1
2
3
4
5
员工小王和小李分别提供了不同的方案.
(1)小王准备用线性回归模型拟合
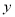 与
与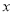 的关系,请你帮助建立
的关系,请你帮助建立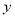 关于
关于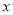 的线性回归方程;(系数精确到0.01)
的线性回归方程;(系数精确到0.01)(2)小李决定选择对数回归模型拟合
 与
与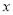 的关系,得到了回归方程:
的关系,得到了回归方程: 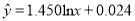 ,并提供了相关指数
,并提供了相关指数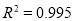 .请用相关指数说明哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析数据
.请用相关指数说明哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析数据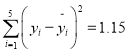 )
)参考公式:相关指数
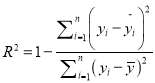
回归方程
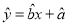 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: 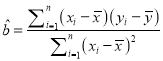 ,
, 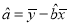 .参考数据:
.参考数据: 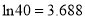 ,
, 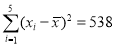 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  .
.(1)求函数
 在
在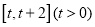 的最小值;
的最小值; (2)若函数
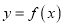 与
与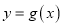 的图象恰有一个公共点,求实数
的图象恰有一个公共点,求实数 的值;
的值;(3)若函数
 有两个不同的极值点
有两个不同的极值点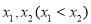 ,且
,且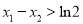 ,求实数
,求实数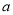 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】有两枚均匀的硬币和一枚不均匀的硬币,其中不均匀的硬币抛掷后出现正面的概率为
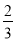 ,小华先抛掷这三枚硬币,然后小红再抛掷这三枚硬币.
,小华先抛掷这三枚硬币,然后小红再抛掷这三枚硬币.(1)求小华抛得一个正面两个反面且小红抛得两个正面一个反面的概率;
(2)若用
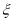 表示小华抛得正面的个数,求
表示小华抛得正面的个数,求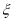 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,曲线
中,曲线 ,曲线
,曲线 为参数), 以坐标原点
为参数), 以坐标原点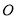 为极点,
为极点,  轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.(1)求曲线
 的极坐标方程;
的极坐标方程;(2)若射线
 分别交
分别交 于
于 两点, 求
两点, 求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求
 的最大值;
的最大值;(2)当
 时,函数
时,函数 有最小值. 记
有最小值. 记 的最小值为
的最小值为 ,求函数
,求函数 的值域.
的值域.
相关试题

