【题目】已知正项等差数列{an}的前n项和为Sn , 且满足 ![]() ,S7=56.
,S7=56.
(1)求数列{an}的通项公式an;
(2)若数列{bn}满足b1=a1且bn+1﹣bn=an+1 , 求数列 ![]() 的前n项和Tn .
的前n项和Tn .
参考答案:
【答案】
(1)解:∵{an}是等差数列且 ![]() ,
,
∴ ![]() ,
,
又∵an>0∴a3=6.
∵ ![]() ,
,
∴d=a4﹣a3=2,
∴an=a3+(n﹣3)d=2n.
(2)解:∵bn+1﹣bn=an+1且an=2n,
∴bn+1﹣bn=2(n+1)
当n≥2时,bn=(bn﹣bn﹣1)+(bn﹣1﹣bn﹣2)+…+(b2﹣b1)+b1
=2n+2(n﹣1)+…+2×2+2=n(n+1),
当n=1时,b1=2满足上式,bn=n(n+1)
∴ ![]()
∴ 
【解析】(1)由已知可得 ![]() ,可求a3 , 利用等差数列的求和公式及性质可求a4 , 则d=a4﹣a3 , 从而可求通项(2)由已知可得bn+1﹣bn=2(n+1),利用叠加法可求bn , 然后利用裂项相消法可求数列的和
,可求a3 , 利用等差数列的求和公式及性质可求a4 , 则d=a4﹣a3 , 从而可求通项(2)由已知可得bn+1﹣bn=2(n+1),利用叠加法可求bn , 然后利用裂项相消法可求数列的和
【考点精析】本题主要考查了等差数列的通项公式(及其变式)和数列的前n项和的相关知识点,需要掌握通项公式:![]() 或
或![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|0<x<3},B=
 ,则集合A∩(RB)为( )
,则集合A∩(RB)为( )
A.[0,1)
B.(0,1)
C.[1,3)
D.(1,3) -
科目: 来源: 题型:
查看答案和解析>>【题目】(
 分)已知椭圆
分)已知椭圆 的左焦点为
的左焦点为 ,过
,过 的直线
的直线 与
与 交于
交于 、
、 两点.
两点.(
 )求椭圆
)求椭圆 的离心率.
的离心率.(
 )当直线
)当直线 与
与 轴垂直时,求线段
轴垂直时,求线段 的长.
的长.(
 )设线段
)设线段 的中点为
的中点为 ,
, 为坐标原点,直线
为坐标原点,直线 交椭圆
交椭圆 交于
交于 、
、 两点,是否存在直线
两点,是否存在直线 使得
使得 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】执行图题实数的程序框图,如果输入a=2,b=2,那么输出的a值为( )

A.44
B.16
C.256
D.log316 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
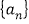 的前
的前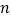 项和为
项和为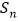 ,公差
,公差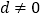 ,且
,且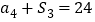 ,
,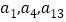 成等比数列.
成等比数列.(1)求数列
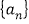 的通项公式;
的通项公式;(2)设
 是首项为1,公比为
是首项为1,公比为 的等比数列,求数列
的等比数列,求数列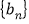 的前
的前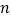 项和
项和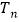 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
 的参数方程是
的参数方程是 (
( 为参数),曲线
为参数),曲线 的参数方程是
的参数方程是 (
( 为参数).
为参数).(Ⅰ)将曲线
 ,
, 的参数方程化为普通方程;
的参数方程化为普通方程;(Ⅱ)求曲线
 上的点到曲线
上的点到曲线 的距离的最大值和最小值.
的距离的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,
, 分别为椭圆的左右焦点,
分别为椭圆的左右焦点, 为椭圆
为椭圆 的短轴顶点,且
的短轴顶点,且 .
.(1)求椭圆的方程
(2)过
 作直线
作直线 交椭圆于
交椭圆于 两点,求
两点,求 的面积的最大值
的面积的最大值
相关试题

