【题目】已知椭圆![]() :
: ![]() ,圆
,圆![]() :
: ![]() 的圆心
的圆心![]() 在椭圆上,点
在椭圆上,点![]() 到椭圆
到椭圆![]() 的右焦点的距离为
的右焦点的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() ,且
,且![]() 交椭圆
交椭圆![]() 于
于![]() 两点,直线
两点,直线![]() 交圆
交圆![]() 于
于![]() ,
, ![]() 两点,且
两点,且![]() 为
为![]() 的中点,求
的中点,求![]() 面积的取值范围.
面积的取值范围.

参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)求椭圆标准方程,一般方法为待定系数法,只需列出两个独立条件,解方程组即可:一是圆心![]() 在椭圆上,即
在椭圆上,即![]() ,二是根据两点间距离公式得
,二是根据两点间距离公式得![]() ,解得
,解得![]() ,
, ![]() ,(2)设直线
,(2)设直线![]() :
: ![]() ,直线
,直线![]() 的方程为
的方程为![]() ,根据几何条件得
,根据几何条件得![]() ,所以△
,所以△![]() 的面积等于
的面积等于![]() ,先根据点到直线距离公式得
,先根据点到直线距离公式得![]() ,再联立直线方程与椭圆方程,结合韦达定理、弦长公式得
,再联立直线方程与椭圆方程,结合韦达定理、弦长公式得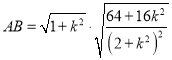 ,即
,即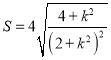 ,最后根据分式函数值域求法得范围
,最后根据分式函数值域求法得范围
试题解析:(1)圆![]() :
: ![]() 的圆心为
的圆心为![]() ,
,
代入椭圆方程可得![]() ,
,
由点![]() 到椭圆
到椭圆![]() 的右焦点的距离为
的右焦点的距离为![]() ,即有
,即有![]() ,
,
解得![]() ,即
,即![]() ,
,
解得![]() ,
, ![]() ,
,
即有椭圆方程为![]() .
.
(2)依题意知直线![]() 斜率必存在,当斜率为0时,直线
斜率必存在,当斜率为0时,直线![]() :
: ![]() ,
,
代入圆的方程可得![]() ,可得
,可得![]() 的坐标为
的坐标为![]() ,又
,又![]() ,
,
可得![]() 的面积为
的面积为![]() ;
;
当直线![]() 斜率不为0时设直线
斜率不为0时设直线![]() :
: ![]() ,代入圆
,代入圆![]() 的方程可得
的方程可得
![]() ,
,
可得中点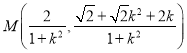 ,
,
 ,
,
此时直线![]() 的方程为
的方程为![]() ,代入椭圆方程,可得:
,代入椭圆方程,可得:
![]() ,
,
设![]() ,
, ![]() ,可得
,可得![]() ,
, ![]() ,
,
则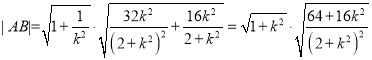 ,
,
可得![]() 的面积为
的面积为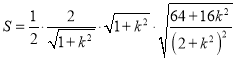
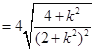 ,
,
设![]() (
(![]() ),可得
),可得 ,
,
可得![]() ,且
,且![]() ,
,
综上可得,△![]() 的面积的取值范围是
的面积的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校调查了20名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是
 ,样本数据分组为
,样本数据分组为 ,
, ,
, ,
, ,
, .
.
(1)求直方图中
 的值;
的值;(2)从每周自习时间在
 的受调查学生中,随机抽取2人,求恰有1人的每周自习时间在
的受调查学生中,随机抽取2人,求恰有1人的每周自习时间在 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
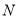 经过点
经过点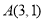 ,
,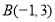 ,且它的圆心在直线
,且它的圆心在直线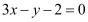 上.
上.(Ⅰ)求圆
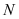 的方程;
的方程; (Ⅱ)求圆
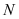 关于直线
关于直线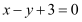 对称的圆的方程。
对称的圆的方程。(Ⅲ)若点
 为圆
为圆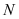 上任意一点,且点
上任意一点,且点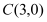 ,求线段
,求线段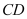 的中点
的中点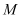 的轨迹方程.
的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
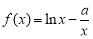 ,
,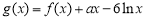 ,其中a∈R.
,其中a∈R.(Ⅰ)当a=1时,判断f(x)的单调性;
(Ⅱ)若g(x)在其定义域内为增函数,求正实数a的取值范围
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC.E是PC的中点,作EF⊥PB交PB于点F.

(1)证明PA∥平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C-PB-D的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-1《几何证明选讲》
已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点

(1)求证:BD平分∠ABC;
(2)若AB=4,AD=6,BD=8,求AH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016 年1 月1 日起全国统一实施全面两孩政策.为了解适龄民众对放开生育二胎政策的态度,某市选取
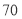 后和
后和 后作为调查对象,随机调查了
后作为调查对象,随机调查了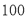 位,得到数据如下表:
位,得到数据如下表: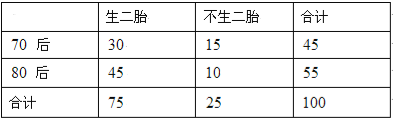
(Ⅰ)以这
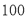 个人的样本数据估计该市的总体数据,且以频率估计概率,若从该市
个人的样本数据估计该市的总体数据,且以频率估计概率,若从该市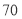 后公民中随机抽取
后公民中随机抽取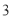 位,记其中生二胎的人数为
位,记其中生二胎的人数为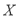 ,求随机变量
,求随机变量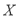 的分布列和数学期望;
的分布列和数学期望;(Ⅱ)根据调查数据,是否有
 以上的把握认为“生二胎与年龄有关”,并说明理由:
以上的把握认为“生二胎与年龄有关”,并说明理由:参考数据:

(参考公式:
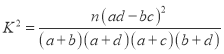 ,其中
,其中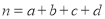 )
)
相关试题

