【题目】已知函数![]() ,
,![]() ,其中a∈R.
,其中a∈R.
(Ⅰ)当a=1时,判断f(x)的单调性;
(Ⅱ)若g(x)在其定义域内为增函数,求正实数a的取值范围
参考答案:
【答案】(Ⅰ)在(0,+∞)上单调递增.(Ⅱ)a≥![]()
【解析】
试题分析:(Ⅰ)求函数导数并确定导函数符号:![]() ,即得函数在定义域上单调递增(Ⅱ)g(x)在其定义域内为增函数,等价于g′(x)≥0恒成立,再利用变量分离法将其转化为对应函数最值:
,即得函数在定义域上单调递增(Ⅱ)g(x)在其定义域内为增函数,等价于g′(x)≥0恒成立,再利用变量分离法将其转化为对应函数最值:![]() 的最大值,最后利用基本不等式求
的最大值,最后利用基本不等式求![]() 最大值
最大值![]() 得正实数a的取值范围
得正实数a的取值范围
试题解析:(1)由![]() 得定义域为(0,+∞),
得定义域为(0,+∞),![]() ,
,
当a=1时,![]() , f(x)在(0,+∞)上单调递增.
, f(x)在(0,+∞)上单调递增.
(2)由已知得, ![]()
因为g(x)在其定义域内为增函数,所以x∈(0,+∞),
g′(x)≥0,即ax2-5x+a≥0,即![]()
而![]() ,当且仅当x=1时,等号成立,
,当且仅当x=1时,等号成立,
所以a≥![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需各种开支2 000元.
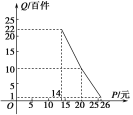
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校调查了20名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是
 ,样本数据分组为
,样本数据分组为 ,
, ,
, ,
, ,
, .
.
(1)求直方图中
 的值;
的值;(2)从每周自习时间在
 的受调查学生中,随机抽取2人,求恰有1人的每周自习时间在
的受调查学生中,随机抽取2人,求恰有1人的每周自习时间在 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
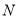 经过点
经过点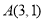 ,
,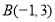 ,且它的圆心在直线
,且它的圆心在直线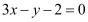 上.
上.(Ⅰ)求圆
 的方程;
的方程; (Ⅱ)求圆
 关于直线
关于直线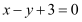 对称的圆的方程。
对称的圆的方程。(Ⅲ)若点
 为圆
为圆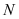 上任意一点,且点
上任意一点,且点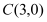 ,求线段
,求线段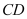 的中点
的中点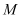 的轨迹方程.
的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  ,圆
,圆 :
:  的圆心
的圆心 在椭圆上,点
在椭圆上,点 到椭圆
到椭圆 的右焦点的距离为
的右焦点的距离为 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)过点
 作互相垂直的两条直线
作互相垂直的两条直线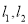 ,且
,且 交椭圆
交椭圆 于
于 两点,直线
两点,直线 交圆
交圆 于
于 ,
,  两点,且
两点,且 为
为 的中点,求
的中点,求 面积的取值范围.
面积的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC.E是PC的中点,作EF⊥PB交PB于点F.

(1)证明PA∥平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C-PB-D的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-1《几何证明选讲》
已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点

(1)求证:BD平分∠ABC;
(2)若AB=4,AD=6,BD=8,求AH的长.
相关试题

