【题目】选修4-1《几何证明选讲》
已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点

(1)求证:BD平分∠ABC;
(2)若AB=4,AD=6,BD=8,求AH的长.
参考答案:
【答案】(1) 详见解析(2)3
【解析】
试题分析:(1) 证明BD平分∠ABC实质就是求角相等:由弦切角定理得CDE=DBC ,由平行得CDE=DCA ,由同弧对等角得DBA=DCA ,三者结合得DBA=DBC (2)求线段长,一般利用相似三角形得比例关系:由ABH∽DBC,得![]() ,而由等角转化为等弦:由DBA=DBC 得AD=DC,
,而由等角转化为等弦:由DBA=DBC 得AD=DC,![]() ,解得AH=3
,解得AH=3
试题解析:证明:(1)∵AC∥DE,∴CDE=DCA,又∵DBA=DCA,∴CDE=DBA
∵直线DE为圆O的切线,∴CDE=DBC
故DBA=DBC,即BD平分∠ABC
(2)∵CAB=CDB,且DBA=DBC,∴ABH∽DBC,∴![]()
又EDC=DAC=DCA,∴AD=DC
∴![]() , ∵AB=4,AD=6,BD=8∴AH=3
, ∵AB=4,AD=6,BD=8∴AH=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
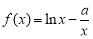 ,
,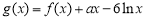 ,其中a∈R.
,其中a∈R.(Ⅰ)当a=1时,判断f(x)的单调性;
(Ⅱ)若g(x)在其定义域内为增函数,求正实数a的取值范围
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  ,圆
,圆 :
:  的圆心
的圆心 在椭圆上,点
在椭圆上,点 到椭圆
到椭圆 的右焦点的距离为
的右焦点的距离为 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)过点
 作互相垂直的两条直线
作互相垂直的两条直线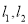 ,且
,且 交椭圆
交椭圆 于
于 两点,直线
两点,直线 交圆
交圆 于
于 ,
,  两点,且
两点,且 为
为 的中点,求
的中点,求 面积的取值范围.
面积的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC.E是PC的中点,作EF⊥PB交PB于点F.

(1)证明PA∥平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C-PB-D的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016 年1 月1 日起全国统一实施全面两孩政策.为了解适龄民众对放开生育二胎政策的态度,某市选取
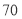 后和
后和 后作为调查对象,随机调查了
后作为调查对象,随机调查了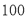 位,得到数据如下表:
位,得到数据如下表: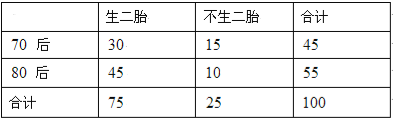
(Ⅰ)以这
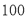 个人的样本数据估计该市的总体数据,且以频率估计概率,若从该市
个人的样本数据估计该市的总体数据,且以频率估计概率,若从该市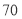 后公民中随机抽取
后公民中随机抽取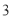 位,记其中生二胎的人数为
位,记其中生二胎的人数为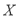 ,求随机变量
,求随机变量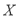 的分布列和数学期望;
的分布列和数学期望;(Ⅱ)根据调查数据,是否有
 以上的把握认为“生二胎与年龄有关”,并说明理由:
以上的把握认为“生二胎与年龄有关”,并说明理由:参考数据:

(参考公式:
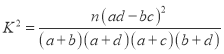 ,其中
,其中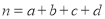 )
) -
科目: 来源: 题型:
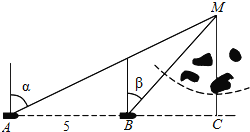
查看答案和解析>>【题目】如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行.
(1)若α=2β=60°,问该船有无触礁危险?
(2)当α与β满足什么条件时,该船没有触礁的危险?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某年级同学每天参加体育锻炼的时间,比较恰当地收集数据的方法是( )
A.查阅资料B.问卷调查C.做试验D.以上均不对
相关试题

