【题目】如图,在三棱柱![]() 与四棱锥
与四棱锥![]() 的组合体中,已知
的组合体中,已知![]() 平面
平面![]() ,四边形
,四边形![]() 是平行四边形,
是平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,设
,设![]() 是线段
是线段![]() 中点.
中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求四棱锥![]() 的体积.
的体积.
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】试题分析:取![]() 的中点
的中点![]() ,连接
,连接![]() ,易证
,易证![]() 为平行四边形,从而得到
为平行四边形,从而得到![]() ,再利用线面平行的判定定理即可;
,再利用线面平行的判定定理即可;
(2)根据![]() ,证得
,证得![]() ,即
,即![]() ,进一步可证
,进一步可证![]() ,从而证得
,从而证得![]() 面
面![]() ,于是得
,于是得![]() 平面
平面![]() ,利用面面垂直的判定定理可得结论;
,利用面面垂直的判定定理可得结论;
(3)利用等体积法,即可求得点![]() 到平面
到平面![]() 的距离.
的距离.
试题解析:
(1)证明:取![]() 的中点
的中点![]() ,连结
,连结![]() ,
, ![]() ,
, ![]() ,则
,则![]() 、
、![]() 、
、![]() 三点共线,
三点共线,
∵![]() 为三棱柱,∴平面
为三棱柱,∴平面![]() 平面
平面![]() ,
,
故![]() 且
且![]() ,∴四边形
,∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,又∵
,又∵![]() 面
面![]() ,
,
![]() 面
面![]() 面
面![]() .
.
(2)证明:∵![]() ,
, ![]() ,
, ![]() ,作
,作![]() 于
于![]() ,
,
可得![]() ,
, ![]() ,
, ![]() ,则
,则![]() ,
,
∴![]() ,即
,即![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
,
在三棱柱![]() 中,
中, ![]() 而
而![]() ,
,
∴![]() 平面
平面![]() ,又
,又![]() ,得
,得![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(3)由(2)知, ![]() ,又
,又![]() ,∴
,∴![]() 平面
平面![]() ,
,
即![]() 为四棱锥
为四棱锥![]() 的高,
的高, ![]() ,又
,又![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知α,β是平面,m,n是直线.下列命题中不正确的是 ( )
A.若m∥n,m⊥α,则n⊥α
B.若m∥α,α∩β=n,则m∥n
C.若m⊥α,m⊥β,则α∥β
D.若m⊥α, ,则α⊥β
,则α⊥β -
科目: 来源: 题型:
查看答案和解析>>【题目】图是正方体的平面展开图,在这个正方体中:①
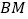 与
与  平行;②
平行;②  与
与  是异面直线;③
是异面直线;③  与
与 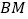 成
成  角;④
角;④  与
与  垂直;以上四个命题中,正确的是( )
垂直;以上四个命题中,正确的是( )
A.①②③
B.②④
C.②③④
D.③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,直线
中,直线  的参数方程为
的参数方程为  (
(  为参数).再以原点为极点,以
为参数).再以原点为极点,以  正半轴为极轴建立极坐标系,并使得它与直角坐标系
正半轴为极轴建立极坐标系,并使得它与直角坐标系  有相同的长度单位.在该极坐标系中圆
有相同的长度单位.在该极坐标系中圆  的方程为
的方程为  .
.
(1)求圆 的直角坐标方程;
的直角坐标方程;
(2)设圆 与直线
与直线  交于点
交于点  、
、  ,若点
,若点  的坐标为
的坐标为  ,求
,求  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
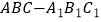 中,侧面
中,侧面  和侧面
和侧面  均为正方形,
均为正方形,  ,D为BC的中点.
,D为BC的中点.
(1)求证: ;
;
(2)求证:
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且


(1)求证:不论 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD ? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 在区间
在区间  上有最大值4和最小值1,
上有最大值4和最小值1,
设 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若不等式 在
在  上恒成立,求实数
上恒成立,求实数  的取值范围.
的取值范围.
相关试题

