【题目】如图,在三棱柱 ![]() 中,侧面
中,侧面 ![]() 和侧面
和侧面 ![]() 均为正方形,
均为正方形, ![]() ,D为BC的中点.
,D为BC的中点.
(1)求证: ![]() ;
;
(2)求证: ![]()
参考答案:
【答案】
(1)证明:连结 ![]() 交
交 ![]() 于点O,则O为
于点O,则O为 ![]() 中点。
中点。
![]() O为BC中点,
O为BC中点,
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
(2)证明: ![]()
![]() ,
, ![]() ,
, ![]()
![]()
![]()
![]()
![]() ,
, ![]() ,
, ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]() 四边形
四边形 ![]() 为正方形,
为正方形, ![]()
![]() ,
,
![]()
![]() ,
, ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
【解析】(1)由已知条件作出辅助线根据中位线的性质找到线线的平行关系,根据线面平行的判定定理即可得证。(2)首先由题意可证出 A1 B2 ⊥ 平 面 A A1 C1 C ,再由线面垂直的性质定理得出 A1 B1 ⊥ A C1 ,结合题意 四边形 A A 1 C1 C 为正方形得出 A 1 C ⊥ A C1,由线面垂直的判定定理可得出
A C 1 ⊥ 平 面 A1 B1 C由线面垂直的定义可得证结果。
【考点精析】本题主要考查了直线与平面平行的判定和直线与平面垂直的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图是正方体的平面展开图,在这个正方体中:①
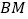 与
与  平行;②
平行;②  与
与  是异面直线;③
是异面直线;③  与
与 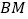 成
成  角;④
角;④  与
与  垂直;以上四个命题中,正确的是( )
垂直;以上四个命题中,正确的是( )
A.①②③
B.②④
C.②③④
D.③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,直线
中,直线  的参数方程为
的参数方程为  (
(  为参数).再以原点为极点,以
为参数).再以原点为极点,以  正半轴为极轴建立极坐标系,并使得它与直角坐标系
正半轴为极轴建立极坐标系,并使得它与直角坐标系  有相同的长度单位.在该极坐标系中圆
有相同的长度单位.在该极坐标系中圆  的方程为
的方程为  .
.
(1)求圆 的直角坐标方程;
的直角坐标方程;
(2)设圆 与直线
与直线  交于点
交于点  、
、  ,若点
,若点  的坐标为
的坐标为  ,求
,求  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
 与四棱锥
与四棱锥 的组合体中,已知
的组合体中,已知 平面
平面 ,四边形
,四边形 是平行四边形,
是平行四边形,  ,
,  ,
,  ,
,  ,设
,设 是线段
是线段 中点.
中点.
(1)求证:
 平面
平面 ;
;(2)证明:平面
 平面
平面 ;
;(3)求四棱锥
 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且


(1)求证:不论 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD ? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 在区间
在区间  上有最大值4和最小值1,
上有最大值4和最小值1,
设 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若不等式 在
在  上恒成立,求实数
上恒成立,求实数  的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某同学用“描点法”画函数
 在区间
在区间 上的图象时,列表并填入了部分数据,如下表:
上的图象时,列表并填入了部分数据,如下表:
(1)请将上表数据补充完整,并在给出的直角坐标系中,画出
 在区间
在区间 上的图象;
上的图象;(2)利用函数的图象,直接写出函数
 在
在 上的单调递增区间;
上的单调递增区间;
(3)将
 图象上所有点向左平移
图象上所有点向左平移 个单位长度,得到
个单位长度,得到 的图象,若
的图象,若 图象的一个对称中心为
图象的一个对称中心为 ,求
,求 的最小值.
的最小值.
相关试题

