【题目】已知函数 ![]() 在区间
在区间 ![]() 上有最大值4和最小值1,
上有最大值4和最小值1,
设 ![]() .
.
(Ⅰ)求 ![]() 的值;
的值;
(Ⅱ)若不等式 ![]() 在
在 ![]() 上恒成立,求实数
上恒成立,求实数 ![]() 的取值范围.
的取值范围.
参考答案:
【答案】解:(Ⅰ) ![]() ,
,
因为 ![]() ,所以
,所以 ![]() 在区间
在区间 ![]() 上是增函数,
上是增函数,
故 ![]() ,解得
,解得 ![]() .
.
(Ⅱ)由已知可得 ![]() ,所以
,所以 ![]() 可化为
可化为 ![]() ,
,
化为 ![]() ,令
,令 ![]() ,则
,则 ![]() ,因
,因 ![]() ,故
,故 ![]() ,
,
记 ![]() ,因为
,因为 ![]() ,故
,故 ![]() ,
,
所以 ![]() 的取值范围是
的取值范围是 ![]()
【解析】(1)由函数可知其图像是开口向上的抛物线对称轴为x=1,所以函数 g(x) 在区间 [ 2 , 3 ] 上单调递增根据二次函数在指定区间上的最值情况代入数值求出a、b的值即可。(2)整理已知的函数代数式转化为 2x + ![]() 2 ≥ k 2x,由整体思想转化为 k ≤ t2 2 t + 1 结合2x>0,x ∈ [ 1 , 1 ]即可 t ∈ [
2 ≥ k 2x,由整体思想转化为 k ≤ t2 2 t + 1 结合2x>0,x ∈ [ 1 , 1 ]即可 t ∈ [ ![]() , 2 ] ,借助二次函数在指定区间上的最值情况求出 h ( t ) min= 0 ,进而得出 k 的取值范围。
, 2 ] ,借助二次函数在指定区间上的最值情况求出 h ( t ) min= 0 ,进而得出 k 的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
 与四棱锥
与四棱锥 的组合体中,已知
的组合体中,已知 平面
平面 ,四边形
,四边形 是平行四边形,
是平行四边形,  ,
,  ,
,  ,
,  ,设
,设 是线段
是线段 中点.
中点.
(1)求证:
 平面
平面 ;
;(2)证明:平面
 平面
平面 ;
;(3)求四棱锥
 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
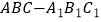 中,侧面
中,侧面  和侧面
和侧面  均为正方形,
均为正方形,  ,D为BC的中点.
,D为BC的中点.
(1)求证: ;
;
(2)求证:
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且


(1)求证:不论 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD ? -
科目: 来源: 题型:
查看答案和解析>>【题目】某同学用“描点法”画函数
 在区间
在区间 上的图象时,列表并填入了部分数据,如下表:
上的图象时,列表并填入了部分数据,如下表:
(1)请将上表数据补充完整,并在给出的直角坐标系中,画出
 在区间
在区间 上的图象;
上的图象;(2)利用函数的图象,直接写出函数
 在
在 上的单调递增区间;
上的单调递增区间;
(3)将
 图象上所有点向左平移
图象上所有点向左平移 个单位长度,得到
个单位长度,得到 的图象,若
的图象,若 图象的一个对称中心为
图象的一个对称中心为 ,求
,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】大西洋鲑鱼每年都要逆流而上,游回产地产卵,研究鲑鱼的科学家发现鲑鱼的游速
 (单位:
(单位:  )与其耗氧量单位数
)与其耗氧量单位数 之间的关系可以表示为函数
之间的关系可以表示为函数 ,其中
,其中 为常数,已知一条鲑鱼在静止时的耗氧量为100个单位;而当它的游速为
为常数,已知一条鲑鱼在静止时的耗氧量为100个单位;而当它的游速为 时,其耗氧量为2700个单位.
时,其耗氧量为2700个单位.(1)求出游速
 与其耗氧量单位数
与其耗氧量单位数 之间的函数解析式;
之间的函数解析式;(2)求当一条鲑鱼的游速不高于
 时,其耗氧量至多需要多少个单位?
时,其耗氧量至多需要多少个单位? -
科目: 来源: 题型:
查看答案和解析>>【题目】四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程和相关系数r,分别得到以下四个结论:
① ②
② 
③ ④
④ 
其中,一定不正确的结论序号是( )
A.②③
B.①④
C.①②③
D.②③④
相关试题

