【题目】已知函数![]() 上为增函数.
上为增函数.
(1)求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:
(1)函数为增函数,则导函数大于零恒成立,据此可得实数![]() 的取值范围是
的取值范围是![]() ;
;
(2)利用题意构造新函数![]() ,结合函数的性质可得实数
,结合函数的性质可得实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(1)由题意![]() ,
,
因为![]() 上为增函数,
上为增函数,
所以![]() 上恒成立,
上恒成立,
即![]() ,所以
,所以![]() ,
,
当k=1时, ![]() 恒大于0,故
恒大于0,故![]() 上单增,符合题意.
上单增,符合题意.
所以k的取值范围为k≤1.
(2)设![]() ,
,
![]() ,令
,令![]() ,
,
由(1)知k≤1,
k=1时, ![]() 在R上递增,不合题意,舍去.
在R上递增,不合题意,舍去.
②当k<1时, ![]() 的变化情况如下表:
的变化情况如下表:
x |
| k | (k,1) | 1 | (1,+ |
| + | 0 | - | 0 | + |
| ↗ | 极大
| ↘ | 极小
| ↗ |
由于![]() ,欲使
,欲使![]() 与
与![]() 图象有三个不同的交点,即方程
图象有三个不同的交点,即方程![]() ,
,
也即![]() 有三个不同的实根。故需
有三个不同的实根。故需![]() 即
即![]()
所以![]() 解得
解得![]() .
.
综上,所求k的范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
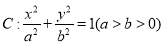 的离心率为
的离心率为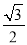 ,且过点
,且过点 .
.(Ⅰ)求椭圆
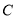 的方程.
的方程.(Ⅱ)若
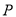 ,
, 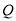 是椭圆
是椭圆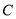 上两个不同的动点,且使
上两个不同的动点,且使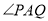 的角平分线垂直于
的角平分线垂直于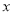 轴,试判断直线
轴,试判断直线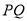 的斜率是否为定值?若是,求出该值;若不是,说明理由.
的斜率是否为定值?若是,求出该值;若不是,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若定义在R上的函数
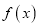 满足
满足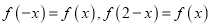 ,且当
,且当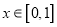 时,
时, 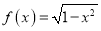 ,则函数
,则函数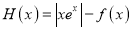 在区间[-7,1]上的零点个数为( )
在区间[-7,1]上的零点个数为( )A. 4 B. 6 C. 8 D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】《中华人民共和国个人所得税》规定,公民月工资、薪金所得不超过3500元的部分不纳税,超过3500元的部分为全月纳税所得额,此项税款按下表分段累计计算:

已知张先生的月工资、薪金所得为10000元,问他当月应缴纳多少个人所得税?
设王先生的月工资、薪金所得为
 元,当月应缴纳个人所得税为
元,当月应缴纳个人所得税为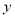 元,写出
元,写出 与
与 的函数关系式;
的函数关系式;(3)已知王先生一月份应缴纳个人所得税为303元,那么他当月的个工资、薪金所得为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量a=
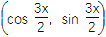 ,b=
,b=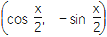 ,且x∈
,且x∈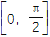 .
.(1)求a·b及|a+b|;
(2)若f(x)=a·b-2λ|a+b|的最小值是-
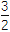 ,求λ的值.
,求λ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4;坐标系与参数方程
在直角坐标系
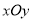 中,直线
中,直线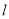 的参数方程为
的参数方程为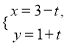 (
(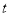 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点, 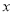 轴正半轴为极轴的极坐标中,曲线
轴正半轴为极轴的极坐标中,曲线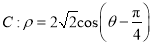 .
.(Ⅰ)求直线
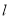 的普通方程和曲线
的普通方程和曲线 的直角坐标方程.
的直角坐标方程.(Ⅱ)求曲线
 上的点到直线
上的点到直线 的距离的最大值.
的距离的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
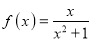 .
.(1)判断并证明函数
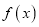 的奇偶性;
的奇偶性;(2)判断当
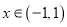 时函数
时函数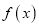 的单调性,并用定义证明;
的单调性,并用定义证明;(3)若
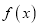 定义域为
定义域为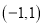 ,解不等式
,解不等式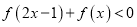 .
.
相关试题

