【题目】已知函数![]() .
.
(1)判断并证明函数![]() 的奇偶性;
的奇偶性;
(2)判断当![]() 时函数
时函数![]() 的单调性,并用定义证明;
的单调性,并用定义证明;
(3)若![]() 定义域为
定义域为![]() ,解不等式
,解不等式![]() .
.
参考答案:
【答案】(1)奇函数(2)增函数(3)![]()
【解析】试题分析:(1)判断与证明函数的奇偶性,首先要确定函数的定义域是否关于原点对称,再判断f(-x)与f(x)的关系,如果对定义域上的任意x,都满足f(-x)=f(x)就是偶函数,如果f(-x)=-f(x)就是奇函数,否则是非奇非偶函数。(2)利函数单调性定义证明单调性,按假设,作差,化简,判断,下结论五个步骤。(3)由(1)(2)奇函数![]() 在(-1,1)为单调函数,
在(-1,1)为单调函数,
原不等式变形为f(2x-1)<-f(x),即f(2x-1)<f(-x),再由函数的单调性及定义(-1,1)求解得x范围。
试题解析:(1)函数![]() 为奇函数.证明如下:
为奇函数.证明如下:
![]() 定义域为
定义域为![]()
又![]()
![]() 为奇函数
为奇函数
(2)函数![]() 在(-1,1)为单调函数.证明如下:
在(-1,1)为单调函数.证明如下:
任取![]() ,则
,则
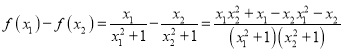
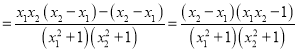
![]()
![]() ,
, ![]()
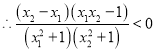
即![]()
故![]() 在(-1,1)上为增函数
在(-1,1)上为增函数
(3)由(1)、(2)可得
![]() 则
则
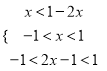 解得:
解得: ![]()
所以,原不等式的解集为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 上为增函数.
上为增函数.(1)求实数
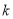 的取值范围;
的取值范围;(2)若函数
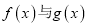 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数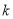 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量a=
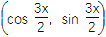 ,b=
,b=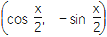 ,且x∈
,且x∈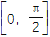 .
.(1)求a·b及|a+b|;
(2)若f(x)=a·b-2λ|a+b|的最小值是-
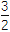 ,求λ的值.
,求λ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4;坐标系与参数方程
在直角坐标系
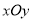 中,直线
中,直线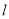 的参数方程为
的参数方程为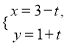 (
(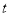 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点, 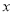 轴正半轴为极轴的极坐标中,曲线
轴正半轴为极轴的极坐标中,曲线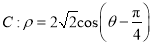 .
.(Ⅰ)求直线
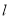 的普通方程和曲线
的普通方程和曲线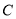 的直角坐标方程.
的直角坐标方程.(Ⅱ)求曲线
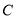 上的点到直线
上的点到直线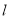 的距离的最大值.
的距离的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 是奇函数,且f(2)=
是奇函数,且f(2)= .
.(1)求实数m和n的值;
(2)判断函数f(x)在(-∞,0)上的单调性,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:极坐标与参数方程
在平面直角坐标系
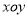 中,直线
中,直线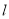 的参数方程为:
的参数方程为: 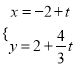 (t为参数),它与曲线C:
(t为参数),它与曲线C: 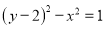 相交于A,B两点.
相交于A,B两点.(1)求|AB|的长;
(2)在以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为
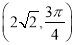 ,求点P到线段AB中点M的距离.
,求点P到线段AB中点M的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:①
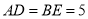 ;②当
;②当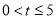 时,
时, 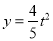 ;③
;③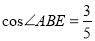 ;④当
;④当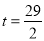 秒时,
秒时,  ∽
∽ ;⑤当
;⑤当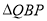 的面积为
的面积为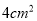 时,时间
时,时间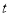 的值是
的值是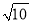 或
或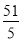 ;其中正确的结论是( )
;其中正确的结论是( )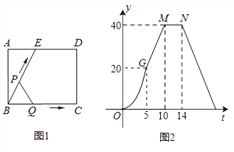
A. ①⑤ B. ②⑤ C. ②③ D. ②④
相关试题

