【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处切线与直线
处切线与直线![]() 垂直(其中
垂直(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() 的解析式及单调减区间;
的解析式及单调减区间;
(2)是否存在常数![]() ,使得对于定义域的任意
,使得对于定义域的任意![]() 恒成立,若存在,求出
恒成立,若存在,求出 ![]() 的值;若
的值;若
不存在,说明理由.
参考答案:
【答案】(1)![]() ,减区间为
,减区间为![]() 和
和![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)借助题设条件运用导数的几何意义求解;(2)借助题设分离参数构造函数运用导数的知识探求.
试题解析:
(1)函数![]() 的定义域为
的定义域为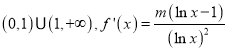 ,又由题意有:
,又由题意有:![]() ,所以
,所以![]() ,故
,故![]() .此时,
.此时,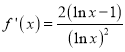 ,由
,由![]() ,解得
,解得![]() 或
或![]() .所以函数
.所以函数![]() 的单调减区间为
的单调减区间为![]() 和
和![]() .
.
(2)要![]() 恒成立,即
恒成立,即![]() ,即
,即![]() .①当
.①当![]() 时,
时,![]() ,则要
,则要![]() 恒成立,令
恒成立,令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 内递减,所以当
内递减,所以当![]() 时,
时,![]() ,故
,故![]() ,所以
,所以![]() 在
在![]() 内递增,
内递增,![]() ,故
,故![]() .②当
.②当![]() 时,
时,![]() , 则要
, 则要![]() 恒成立. 由①可知,当
恒成立. 由①可知,当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 内递增,所以当
内递增,所以当![]() 时,
时,![]() ,故
,故![]() ,所以
,所以![]() 在
在![]() 内递增,
内递增,![]() ,故
,故![]() . 综合① ②可得:
. 综合① ②可得:![]() , 即存在常数
, 即存在常数![]() 满足题意.
满足题意.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随机抽取了40辆汽车在经过路段上某点是的车速(
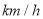 ),现将其分成六段:
),现将其分成六段: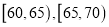 ,
,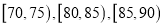 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.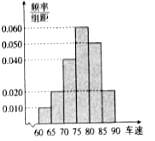
(I)现有某汽车途经该点,则其速度低于80
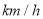 的概率约是多少?
的概率约是多少?(II)根据频率分布直方图,抽取的40辆汽车经过该点的平均速度是多少?
(III)在抽取的40辆汽车且速度在
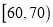 (
(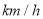 )内的汽车中任取2辆,求这2辆车车速都在
)内的汽车中任取2辆,求这2辆车车速都在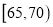 (
(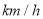 )内的概率.
)内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知函数
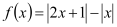 .
.(I)求证:
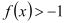 恒成立;
恒成立;(II)若存在实数
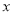 ,使得
,使得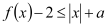 ,求实数
,求实数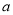 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设锐角三角形的内角
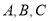 的对边分别为
的对边分别为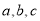 ,且
,且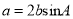 .
.(1)求
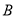 的大小;
的大小;(2)求
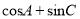 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知流程图如下图所示,该程序运行后,为使输出的
 值为16,则循环体的判断框内①处应填( )
值为16,则循环体的判断框内①处应填( )
A. 2 B. 3 C. 5 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】“开门大吉”是某电视台推出的游戏益智节目.选手面对
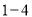 号
号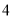 扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金.(奖金金额累加)但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:
扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金.(奖金金额累加)但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段: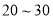 ;
;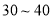 (单位:岁),其猜对歌曲名称与否人数如图所示.
(单位:岁),其猜对歌曲名称与否人数如图所示.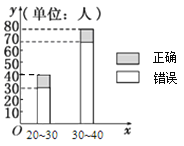
(1)写出
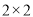 列联表:判断是否有
列联表:判断是否有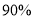 的把握认为猜对歌曲名称与否与年龄有关?
的把握认为猜对歌曲名称与否与年龄有关?说明你的理由.(下面的临界值表供参考)

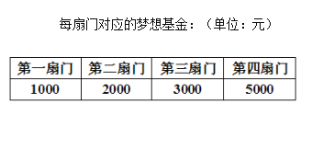
(2)若某选手能正确回答第一、二、三、四扇门的概率分别为
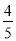 ,
,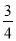 ,
,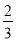 ,
,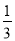 ,正确回答一个问题后,选择继续回答下一个问题的概率是
,正确回答一个问题后,选择继续回答下一个问题的概率是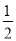 ,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为
,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为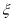 ,求
,求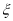 的分布列及数学期望.
的分布列及数学期望.(参考公式
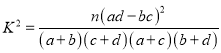 其中
其中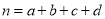 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
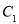 :
: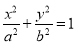 (
(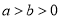 )的离心率为
)的离心率为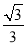 ,连接椭圆的四个顶点得到的四边形的面积为
,连接椭圆的四个顶点得到的四边形的面积为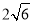 .
.(1)求椭圆
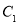 的方程;
的方程;(2)设椭圆
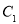 的左焦点为
的左焦点为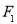 ,右焦点为
,右焦点为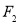 ,直线
,直线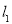 过点
过点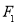 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线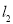 垂直
垂直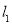 于点
于点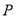 ,线段
,线段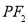 的垂直平分线交
的垂直平分线交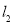 于点
于点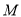 ,求点
,求点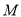 的轨迹
的轨迹 的方程;
的方程;(3)设
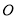 为坐标原点,取
为坐标原点,取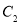 上不同于
上不同于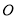 的点
的点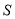 ,以
,以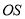 为直径作圆与
为直径作圆与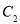 相交另外一点
相交另外一点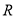 ,求该圆面积的最小值时点
,求该圆面积的最小值时点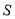 的坐标.
的坐标.
相关试题

