【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,
为参数,![]() ),其中
),其中![]() ,在以
,在以![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() ,曲线
,曲线![]() .
.
(Ⅰ)求![]() 与
与![]() 交点的直角坐标系;
交点的直角坐标系;
(Ⅱ)若![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的最大值.
的最大值.
参考答案:
【答案】(1)交点坐标为![]() ,
, ![]() .(2)最大值为
.(2)最大值为![]() .
.
【解析】试题分析:(1)根据![]() 将曲线
将曲线![]() 与
与![]() 的极坐标方程化为直角坐标方程,再联立方程组求解交点的直角坐标,(2)曲线
的极坐标方程化为直角坐标方程,再联立方程组求解交点的直角坐标,(2)曲线![]() 为直线,倾斜角为
为直线,倾斜角为![]() ,极坐标方程为
,极坐标方程为![]() ,代入
,代入![]() 与
与![]() 的极坐标方程可得
的极坐标方程可得![]() 的极坐标,则
的极坐标,则![]() 为对应极径之差的绝对值,即
为对应极径之差的绝对值,即![]() ,最后根据三角函数关系有界性求最值.
,最后根据三角函数关系有界性求最值.
试题解析:解:(Ⅰ) ![]() :
: ![]() ,
, ![]() :
: ![]() ,
,
联立得交点坐标为![]() ,
, ![]() .
.
(Ⅱ)曲线![]() 的极坐标方程为
的极坐标方程为![]() ,其中
,其中![]() .
.
因此得到![]() 的极坐标为
的极坐标为![]() ,
,
![]() 的极坐为
的极坐为![]() .
.
所以![]() ,
,
当![]() 时,
时, ![]() 取得最大值,最大值为
取得最大值,最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了研究家用轿车在高速公路上的车速情况,交通部门对
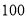 名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在
名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在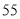 名男性驾驶员中,平均车速超过
名男性驾驶员中,平均车速超过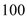
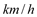 的有
的有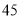 人,不超过
人,不超过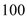
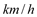 的有
的有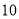 人;在
人;在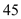 名女性驾驶员中,平均车速超过
名女性驾驶员中,平均车速超过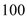
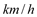 的有
的有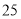 人,不超过
人,不超过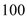
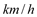 的有
的有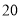 人.
人.(Ⅰ)完成下面的列联表,并判断是否有
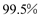 的把握认为平均车速超过100
的把握认为平均车速超过100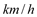 与性别有关;
与性别有关;平均车速超过
 人数
人数平均车速不超过
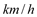 人数
人数合计
男性驾驶人数
女性驾驶人数
合计
(Ⅱ)在被调查的驾驶员中,按分层抽样的方法从平均车速不超过
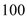
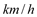 的人中抽取
的人中抽取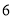 人,再从这
人,再从这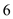 人中采用简单随机抽样的方法随机抽取
人中采用简单随机抽样的方法随机抽取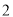 人,求这
人,求这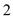 人恰好为
人恰好为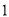 名男生、
名男生、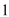 名女生的概率.
名女生的概率.参考公式与数据:
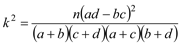 ,其中
,其中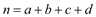 .
.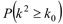
0.150
0.100
0.050
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为R的函数f(x)=
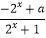 是奇函数,
是奇函数,
(1)求实数a的值;
(2)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求实数k的取值范围;
(3)设关于x的方程f(4x﹣b)+f(﹣2x+1)=0有实数根,求实数b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知椭圆C:
 (m>0)的离心率为
(m>0)的离心率为 ,A,B分别为椭圆的左、右顶点,F是其右焦点,P是椭圆C上异于A、B的动点.
,A,B分别为椭圆的左、右顶点,F是其右焦点,P是椭圆C上异于A、B的动点.(1)求m的值及椭圆的准线方程;
(2)设过点B且与x轴的垂直的直线交AP于点D,当直线AP绕点A转动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为R的函数f(x)在(2,+∞)为增函数,且函数y=f(x+2)为偶函数,则下列结论不成立的是( )
A.f(0)>f(1)
B.f(0)>f(2)
C.f(1)>f(3)
D.f(1)>f(2) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知动点 P 与定点
 的距离和它到定直线 x 4 的距离的比是1: 2 ,记动点 P 的轨迹为曲线 E.
的距离和它到定直线 x 4 的距离的比是1: 2 ,记动点 P 的轨迹为曲线 E.(1)求曲线 E 的方程;
(2)设 A 是曲线 E 上的一个点,直线 AF 交曲线 E 于另一点 B,以 AB 为边作一个平行四边形,顶点 A、B、C、D 都在轨迹 E 上,判断平行四边形 ABCD 能否为菱形,并说明理由;
(3)当平行四边形 ABCD 的面积取到最大值时,判断它的形状,并求出其最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知幂函数y=
 (m∈Z)的图象与x轴,y轴没有交点,且关于y轴对称,则m=( )
(m∈Z)的图象与x轴,y轴没有交点,且关于y轴对称,则m=( )
A.1
B.0,2
C.﹣1,1,3
D.0,1,2
相关试题

