【题目】为了研究家用轿车在高速公路上的车速情况,交通部门对![]() 名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在
名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在![]() 名男性驾驶员中,平均车速超过
名男性驾驶员中,平均车速超过![]()
![]() 的有
的有![]() 人,不超过
人,不超过![]()
![]() 的有
的有![]() 人;在
人;在![]() 名女性驾驶员中,平均车速超过
名女性驾驶员中,平均车速超过![]()
![]() 的有
的有![]() 人,不超过
人,不超过![]()
![]() 的有
的有![]() 人.
人.
(Ⅰ)完成下面的列联表,并判断是否有![]() 的把握认为平均车速超过100
的把握认为平均车速超过100![]() 与性别有关;
与性别有关;
平均车速超过 | 平均车速不超过 | 合计 | |
男性驾驶人数 | |||
女性驾驶人数 | |||
合计 |
(Ⅱ)在被调查的驾驶员中,按分层抽样的方法从平均车速不超过![]()
![]() 的人中抽取
的人中抽取![]() 人,再从这
人,再从这![]() 人中采用简单随机抽样的方法随机抽取
人中采用简单随机抽样的方法随机抽取![]() 人,求这
人,求这![]() 人恰好为
人恰好为![]() 名男生、
名男生、![]() 名女生的概率.
名女生的概率.
参考公式与数据:![]() ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考答案:
【答案】(1)有![]() 的把握认为(2)
的把握认为(2)![]() .
.
【解析】试题分析:(1)将数据对应代入卡方公式,计算出![]() ,再与参考数据比较进行判断,(2)利用枚举法确定从这
,再与参考数据比较进行判断,(2)利用枚举法确定从这![]() 人中随机抽取
人中随机抽取![]() 人的总事件数,再从中挑出恰好为
人的总事件数,再从中挑出恰好为![]() 名男生、
名男生、![]() 名女生事件数,最后根据古典概型概率计算公式求概率
名女生事件数,最后根据古典概型概率计算公式求概率
试题解析:解:(Ⅰ)根据题目中的数据,填写列联表如下:
平均车速超过 | 平均车速不超过 | 合计 | |
男性驾驶员人数 |
|
|
|
女性驾驶员人数 |
|
|
|
合计 |
|
|
|
因为, ![]() ,
,
所以有![]() 的把握认为平均车速超过
的把握认为平均车速超过![]() km/h与性别有关.
km/h与性别有关.
(Ⅱ)由题意抽取![]() 人中,女性
人中,女性![]() 人,男性
人,男性![]() 人,分别设为
人,分别设为![]() 和
和![]() 2,
2,
从这![]() 人中随机抽取
人中随机抽取![]() 人得样本空间:
人得样本空间:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
样本空间数是![]() ,
,
其中这![]() 人恰好为
人恰好为![]() 名男生、
名男生、![]() 名女生的样本数是
名女生的样本数是![]() ,
,
因此这![]() 人恰好为
人恰好为![]() 名男生、
名男生、![]() 名女生的概率是
名女生的概率是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y=lg(3﹣4x+x2)的定义域为M.当x∈M时,求f(x)=2x+2﹣3×4x的最值及相应的x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)满足f(0)=2和f(x+1)﹣f(x)=2x﹣1对任意实数x都成立.
(1)求函数f(x)的解析式;
(2)当t∈[﹣1,3]时,求y=f(2t)的值域. -
科目: 来源: 题型:
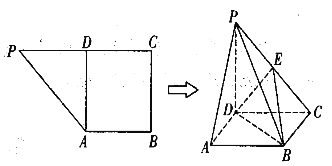
查看答案和解析>>【题目】如图,在直角梯形
 中,
中, ,
, 是
是 的中点,将
的中点,将 沿
沿 折起,使得
折起,使得 平面
平面 .
.
(Ⅰ)求证:平面
 平面
平面  ;
;(Ⅱ)若
 是
是 的中点,求三棱锥
的中点,求三棱锥 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为R的函数f(x)=
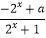 是奇函数,
是奇函数,
(1)求实数a的值;
(2)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求实数k的取值范围;
(3)设关于x的方程f(4x﹣b)+f(﹣2x+1)=0有实数根,求实数b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知椭圆C:
 (m>0)的离心率为
(m>0)的离心率为 ,A,B分别为椭圆的左、右顶点,F是其右焦点,P是椭圆C上异于A、B的动点.
,A,B分别为椭圆的左、右顶点,F是其右焦点,P是椭圆C上异于A、B的动点.(1)求m的值及椭圆的准线方程;
(2)设过点B且与x轴的垂直的直线交AP于点D,当直线AP绕点A转动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,曲线
中,曲线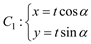 (
(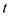 为参数,
为参数,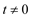 ),其中
),其中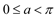 ,在以
,在以 为极点,
为极点,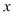 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线 ,曲线
,曲线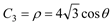 .
.(Ⅰ)求
 与
与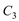 交点的直角坐标系;
交点的直角坐标系;(Ⅱ)若
 与
与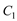 相交于点
相交于点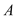 ,
,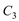 与
与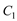 相交于点
相交于点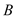 ,求
,求 的最大值.
的最大值.
相关试题

