【题目】如图所示,已知直二面角α﹣AB﹣β,P∈α,Q∈β,PQ与平面α,β所成的角都为30°,PQ=4,PC⊥AB,C为垂足,QD⊥AB,D为垂足,求: 
(1)直线PQ与CD所成角的大小
(2)四面体PCDQ的体积.
参考答案:
【答案】
(1)解:直二面角α﹣AB﹣β,P∈α,Q∈β,PQ与平面α,β所成的角都为30°,PQ=4,PC⊥AB,C为垂足,QD⊥AB,D为垂足,设直线AB与CD所成的角为θ,则由PC⊥AB,cos∠DCQ= ![]() =
= ![]() =
= ![]() ,
,
可知PC⊥β知:cosθ=cos∠PQCcos∠DCQ=cos30° ![]() =
= ![]() ,
,
故θ=45°
(2)解:由题意可知三棱锥的高为PC=2,底面CQD的面积为: ![]() CDDQ=
CDDQ= ![]() =2
=2 ![]() ,
,
三棱锥的体积为: ![]() =
= ![]()
【解析】(1)直接根据PC⊥β以及常用的结论:cosθ=cos∠PQCcos∠DCQ即可求出结果;(2)求出几何体的高与底面面积,即可求解几何体的体积.
【考点精析】认真审题,首先需要了解异面直线及其所成的角(异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系).
-
科目: 来源: 题型:
查看答案和解析>>【题目】设全集为R,集合A={x|﹣3≤x<6},B={x|2<x<9}.
(1)求A∩B,A∪(RB);
(2)已知C={x|a<x<2a+1},若CA,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的前n项和为Sn , n∈N* , 已知a1=1,a2=
 ,a3=
,a3=  ,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn﹣1 .
,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn﹣1 .
(1)求a4的值.
(2)证明:{an﹣1﹣ an}为等比数列;
an}为等比数列;
(3)求数列{an}的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,
 .
.
(1)求 的值;
的值;
(2)当△ABC的面积最大时,求∠A的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 .
.
(1)画出函数f(x)图象;
(2)求f(﹣a2﹣1)(a∈R),f(f(3))的值;
(3)当﹣4≤x<3时,求f(x)取值的集合. -
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两个班进行数学考试,按照大于等于120分为优秀,120分以下为非优秀统计成绩后,得到如下
 列联表:(单位:人).
列联表:(单位:人). 
已知在全部105人中随机抽取1人成绩是优秀的概率为
 .
.(1)请完成上面的
 列联表,并根据表中数据判断,是否有
列联表,并根据表中数据判断,是否有 的把握认为“成绩与班级有关系”?
的把握认为“成绩与班级有关系”?(2)若甲班优秀学生中有男生6名,女生4名,现从中随机选派3名学生参加全市数学竞赛,记参加竞赛的男生人数为
 ,求
,求 的分布列与期望.
的分布列与期望.附:
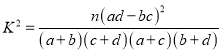

0.15
0.10
0.050
0.010

2.072
2.706
3.841
6.635
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xm﹣
 ,且f(3)=
,且f(3)=  .
.
(1)求函数f(x)的解析式,并判断函数f(x)的奇偶性.
(2)证明函数f(x)在(0,+∞)上的单调性.
相关试题

