【题目】设全集为R,集合A={x|﹣3≤x<6},B={x|2<x<9}.
(1)求A∩B,A∪(RB);
(2)已知C={x|a<x<2a+1},若CA,求实数a的取值范围.
参考答案:
【答案】
(1)解:集合A={x|﹣3≤x<6},B={x|2<x<9}.
由数轴得A∩B={x|2<x<6},
因为RB={x|x≤2或x≥9},
所以A∪(RB)={x|x<6或x≥9};
(2)解:C={x|a<x<2a+1},CA,
若C=,则a≥2a+1,即a≤﹣1,满足题意,
若C≠,则 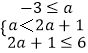 ,解得﹣1
,解得﹣1 ![]() ,
,
综上可知,实数a的取值范围为a ![]()
【解析】(1)直接利用交集求解A∩B,求出B的补集,然后求解A∪(RB);(2)利用子集关系列出不等式组求解即可.
【考点精析】关于本题考查的交、并、补集的混合运算,需要了解求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(sinx+cosx)2+cos2x
(1)求f(x)最小正周期;
(2)求f(x)在区间[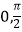 ]上的最大值和最小值.
]上的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,与y=
 的奇偶性和单调性都相同的是( )
的奇偶性和单调性都相同的是( )
A.f(x)=x﹣1
B.f(x)=x
C.f(x)=x2
D.f(x)=x3 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=x3+3x2+1,已知a≠0,且f(x)﹣f(a)=(x﹣b)(x﹣a)2 , x∈R,则实数a= , b= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的前n项和为Sn , n∈N* , 已知a1=1,a2=
 ,a3=
,a3=  ,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn﹣1 .
,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn﹣1 .
(1)求a4的值.
(2)证明:{an﹣1﹣ an}为等比数列;
an}为等比数列;
(3)求数列{an}的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,
 .
.
(1)求 的值;
的值;
(2)当△ABC的面积最大时,求∠A的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知直二面角α﹣AB﹣β,P∈α,Q∈β,PQ与平面α,β所成的角都为30°,PQ=4,PC⊥AB,C为垂足,QD⊥AB,D为垂足,求:

(1)直线PQ与CD所成角的大小
(2)四面体PCDQ的体积.
相关试题

