【题目】如图,四边形![]() 是边长为4的正方形,点
是边长为4的正方形,点![]() 为
为![]() 边上任意一点(与点
边上任意一点(与点![]() 不重合),连接
不重合),连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,设
,设![]() .
.
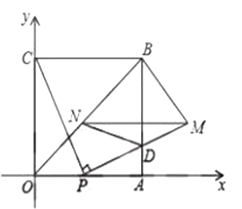
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示)
的代数式表示)
(2)试判断线段![]() 的长度是否随点
的长度是否随点![]() 的位置的变化而改变?并说明理由.
的位置的变化而改变?并说明理由.
(3)当![]() 为何值时,四边形
为何值时,四边形![]() 的面积最小.
的面积最小.
(4)在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使得
,使得![]() 是等腰三角形,请直接写出不少于4个符合条件的点
是等腰三角形,请直接写出不少于4个符合条件的点![]() 的坐标(用含
的坐标(用含![]() 的式子表示)
的式子表示)
参考答案:
【答案】(1)![]() (2)
(2)![]() 的长度不变(3)
的长度不变(3)![]() (4)
(4)![]()
![]() ,
, ![]() ,
, ![]()
【解析】【试题分析】(1)作![]() 于点
于点![]() ,依据
,依据![]() ,及
,及![]() ,推得
,推得![]() ,即
,即![]() ,进而依据
,进而依据![]() ,推得
,推得![]() ,借助
,借助![]() ,推出
,推出![]() ≌
≌![]() (
(![]() ),求出
),求出![]() ,
, ![]() ,则
,则![]()
进而求出点![]() 的坐标为
的坐标为![]() ;(2)借助
;(2)借助![]() ,点
,点![]() ,求出直线
,求出直线![]() 的解析式为:
的解析式为: ![]() ,然后再依据点
,然后再依据点![]() 在直线
在直线![]() 上,且
上,且![]() ,求得
,求得![]() ,进而得到点
,进而得到点![]() ,从而求出
,从而求出![]() ,即
,即![]() 的长度不变;(3)借助(1)的结论
的长度不变;(3)借助(1)的结论![]() ,及
,及![]() ,推得
,推得![]() ∽
∽![]() ,故
,故![]() ,从而求得
,从而求得![]() ,
, ![]() ,
, ![]() ,建立函数
,建立函数![]() ,求出当
,求出当![]() 时,四边形
时,四边形![]() 的面积最小,最小值6;(4)借助图形的直观可以探求出在
的面积最小,最小值6;(4)借助图形的直观可以探求出在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使得
,使得![]() 是等腰三角形,此时点
是等腰三角形,此时点![]() 的坐标为:
的坐标为: ![]() ,
, ![]() ,
, ![]() ,
, ![]() :
:
解:(1)作![]() 于点
于点![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,∵
,∵![]() ,
,
∴![]() ≌
≌![]() (
(![]() )
)
∴![]() ,
, ![]() ,∴
,∴![]()
∴点![]() 的坐标为
的坐标为![]() .
.
(2)线段![]() 长度不变.
长度不变.
∵![]() ,点
,点![]() ,∴直线
,∴直线![]() 的解析式为:
的解析式为: ![]() ,
,
∵点![]() 在直线
在直线![]() 上,且
上,且![]() ,
, ![]() ,∴点
,∴点![]()
∴![]() ,即
,即![]() 的长度不变.
的长度不变.
(3)由(1)知, ![]() ,又∵
,又∵![]()
∴![]() ∽
∽![]() ,∴
,∴![]() ,
,
∵![]() ,
, ![]() ,∴
,∴![]()
∴![]() ,得
,得![]() ,
,
∴![]()
∵![]() ,
, ![]() ,
, ![]()
∴![]()
∴当![]() 时,四边形
时,四边形![]() 的面积最小,最小值6;
的面积最小,最小值6;
(4)在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使得
,使得![]() 是等腰三角形,此时点
是等腰三角形,此时点![]() 的坐标为:
的坐标为: ![]() ,
, ![]() ,
, ![]() ,
, ![]()
-
科目: 来源: 题型:
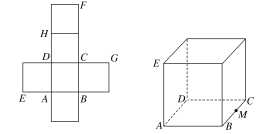
查看答案和解析>>【题目】一个正方体的平面展开图及该正方体直观图的示意图如图所示,在正方体中,设BC的中点为M,GH的中点为N。
(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);
(2)证明:直线MN∥平面BDH;
(3)过点M,N,H的平面将正方体分割为两部分,求这两部分的体积比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
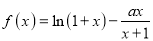 ,
, 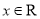 .
.(1)若曲线
 在点
在点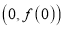 处的切线的斜率为5,求
处的切线的斜率为5,求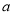 的值;
的值;(2)若函数
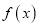 的最小值为
的最小值为 ,求
,求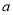 的值;
的值;(3)当
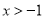 时,
时, 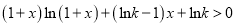 恒成立,求实数
恒成立,求实数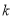 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知长方形ABCD中,AB=1,AD=
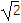 。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.
。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.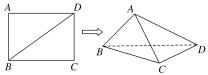
(1)试问:在折叠的过程中,异面直线AB与CD,AD与BC能否垂直?若能垂直,求出相应的a值;若不垂直,请说明理由.
(2)当四面体ABCD的体积最大时,求二面角ACDB的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正整数
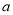 ,
, 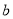 ,
, 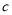 是等腰三角形的三边长,并且
是等腰三角形的三边长,并且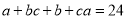 ,这样的三角形有( )个.
,这样的三角形有( )个.A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产的某种时令商品每件成本为
 元,经过市场调研发现,这种商品在未来
元,经过市场调研发现,这种商品在未来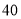 天内的日销售量
天内的日销售量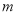 (件)与时间
(件)与时间 (天)的关系如下表所示.
(天)的关系如下表所示.时间
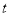 /天
/天1
3
6
10
36
……
日销售量
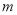 /件
/件94
90
84
76
24
……
未来40天内,前20天每天的价格
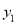 (元/件)与时间
(元/件)与时间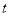 (天)的函数关系式为
(天)的函数关系式为 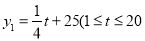 ,且
,且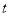 为整数),后20天每天的价格
为整数),后20天每天的价格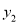 (元/件)与时间
(元/件)与时间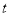 (天)的函数关系式为
(天)的函数关系式为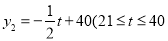 ,且
,且 为整数).
为整数).(Ⅰ)认真分析表格中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据
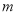 (件)与
(件)与 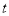 (天)的关系式;
(天)的关系式;(Ⅱ)试预测未来 40 天中哪一天的日销售利润最大,最大利润是多少?
(Ⅲ)在实际销售的前 20 天中,该公司决定每销售 1 件商品就捐赠
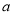 元利润
元利润 给希望工程. 公司通过销售记录发现,前 20 天中,每天扣除捐赠后的日销售利润随时间
给希望工程. 公司通过销售记录发现,前 20 天中,每天扣除捐赠后的日销售利润随时间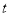 (天)的增大而增大,求
(天)的增大而增大,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
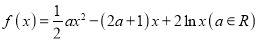 .
.(1)若曲线
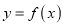 在
在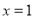 和
和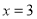 处的切线互相平行,求
处的切线互相平行,求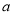 的值;
的值;(2)求
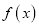 的单调区间;
的单调区间;(3)设
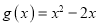 ,若对任意
,若对任意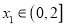 ,均存在
,均存在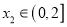 ,使得
,使得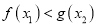 ,求
,求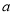 的取值范围.
的取值范围.
相关试题

