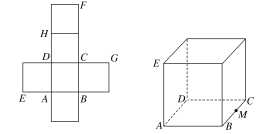
【题目】一个正方体的平面展开图及该正方体直观图的示意图如图所示,在正方体中,设BC的中点为M,GH的中点为N。
(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);
(2)证明:直线MN∥平面BDH;
(3)过点M,N,H的平面将正方体分割为两部分,求这两部分的体积比.
参考答案:
【答案】见解析
【解析】解:(1)点F,G,H的位置如图所示.

(2)证明:连接BD,设O为BD的中点,连接OM,OH,AC,BH,MN。
∵M,N分别是BC,GH的中点,
∴OM∥CD,且OM=![]() CD,NH∥CD,且NH=
CD,NH∥CD,且NH=![]() CD,
CD,
∴OM∥NH,OM=NH,
则四边形MNHO是平行四边形,∴MN∥OH,
又∵MN平面BDH,OH平面BDH,
∴MN∥平面BDH。
(3)由(2)知OM∥NH,OM=NH,连接GM,MH,过点M,N,H的平面就是平面GMH,它将正方体分割为两个同高的棱柱,高都是GH,底面分别是四边形BMGF和三角形MGC,
体积比等于底面积之比,即3∶1。
-
科目: 来源: 题型:
查看答案和解析>>【题目】5名男生4名女生站成一排,求满足下列条件的排法:
(1)女生都不相邻有多少种排法?
(2)男生甲、乙、丙排序一定(只考虑位置的前后顺序),有多少种排法?
(3)男甲不在首位,男乙不在末位,有多少种排法?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数f(x),若存在x0∈R,使得f(x0)=x0成立,则称x0为f(x)的天宫一号点.已知函数f(x)=ax2+(b-7)x+18的两个天宫一号点分别是-3和2.
(1)求a,b的值及f(x)的表达式;
(2)当函数f(x)的定义域是[t,t+1]时,求函数f(x)的最大值g(t).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
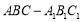 中,侧棱垂直底面,
中,侧棱垂直底面,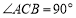 ,
,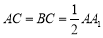 ,
,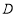 是棱
是棱 的中点.
的中点.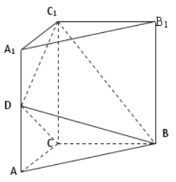
(Ⅰ)证明:平面
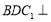 平面
平面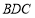 .
.(Ⅱ)平面
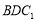 分此棱柱为两部分,求这两部分体积比.
分此棱柱为两部分,求这两部分体积比. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
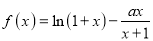 ,
, 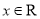 .
.(1)若曲线
 在点
在点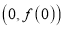 处的切线的斜率为5,求
处的切线的斜率为5,求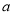 的值;
的值;(2)若函数
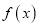 的最小值为
的最小值为 ,求
,求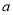 的值;
的值;(3)当
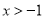 时,
时, 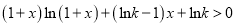 恒成立,求实数
恒成立,求实数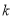 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知长方形ABCD中,AB=1,AD=
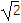 。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.
。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.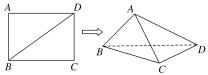
(1)试问:在折叠的过程中,异面直线AB与CD,AD与BC能否垂直?若能垂直,求出相应的a值;若不垂直,请说明理由.
(2)当四面体ABCD的体积最大时,求二面角ACDB的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
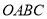 是边长为4的正方形,点
是边长为4的正方形,点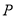 为
为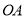 边上任意一点(与点
边上任意一点(与点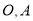 不重合),连接
不重合),连接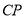 ,过点
,过点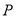 作
作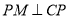 交
交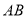 于点
于点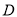 ,且
,且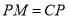 ,过点
,过点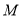 作
作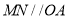 ,交
,交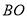 于点
于点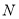 ,连接
,连接 ,设
,设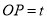 .
.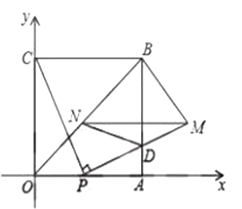
(1)求点
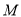 的坐标(用含
的坐标(用含 的代数式表示)
的代数式表示)(2)试判断线段
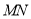 的长度是否随点
的长度是否随点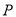 的位置的变化而改变?并说明理由.
的位置的变化而改变?并说明理由.(3)当
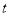 为何值时,四边形
为何值时,四边形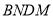 的面积最小.
的面积最小.(4)在
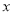 轴正半轴上存在点
轴正半轴上存在点 ,使得
,使得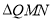 是等腰三角形,请直接写出不少于4个符合条件的点
是等腰三角形,请直接写出不少于4个符合条件的点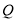 的坐标(用含
的坐标(用含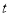 的式子表示)
的式子表示)
相关试题

