【题目】正整数![]() ,
, ![]() ,
, ![]() 是等腰三角形的三边长,并且
是等腰三角形的三边长,并且![]() ,这样的三角形有( )个.
,这样的三角形有( )个.
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】C
【解析】![]() 可以化为(a+b)(c+1)=24,其中a,b,c都是正整数,并且其中两个数相等,
可以化为(a+b)(c+1)=24,其中a,b,c都是正整数,并且其中两个数相等,
令a+b=A,c+1=C则A,C为大于2的正整数,
那么24分解为大于等于2的两个正整数的乘积有几种组合2×12,3×8,4×6,6×4,3×8,2×12,
①、A=2,C=12时,c=11,a+b=2,无法得到满足等腰三角形的整数解;
②、A=3,C=8时,c=7,a+b=3,无法得到满足等腰三角形的整数解;
③、A=4,C=6时,c=5,a+b=4,无法得到满足等腰三角形的整数解;
④、A=6,C=4时,c=3,a+b=6,可以得到a=b=c=3,可以组成等腰三角形;
⑤、A=8,C=3时,c=2,a+b=8,可得a=b=4,c=2,可以组成等腰三角形,a=b=4是两个腰;
⑥、A=12,C=2时,可得a=b=6,c=1,可以组成等腰三角形,a=b=6是两个腰。
∴一共有3个这样的三角形。
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
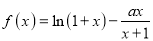 ,
, 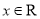 .
.(1)若曲线
 在点
在点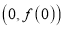 处的切线的斜率为5,求
处的切线的斜率为5,求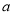 的值;
的值;(2)若函数
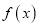 的最小值为
的最小值为 ,求
,求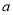 的值;
的值;(3)当
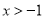 时,
时, 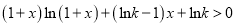 恒成立,求实数
恒成立,求实数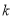 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知长方形ABCD中,AB=1,AD=
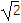 。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.
。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.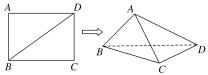
(1)试问:在折叠的过程中,异面直线AB与CD,AD与BC能否垂直?若能垂直,求出相应的a值;若不垂直,请说明理由.
(2)当四面体ABCD的体积最大时,求二面角ACDB的余弦值.
-
科目: 来源: 题型:
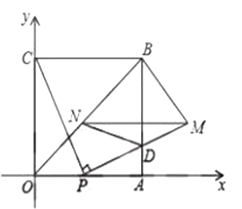
查看答案和解析>>【题目】如图,四边形
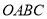 是边长为4的正方形,点
是边长为4的正方形,点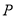 为
为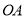 边上任意一点(与点
边上任意一点(与点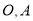 不重合),连接
不重合),连接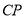 ,过点
,过点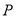 作
作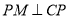 交
交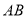 于点
于点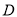 ,且
,且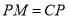 ,过点
,过点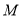 作
作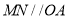 ,交
,交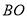 于点
于点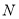 ,连接
,连接 ,设
,设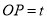 .
.
(1)求点
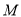 的坐标(用含
的坐标(用含 的代数式表示)
的代数式表示)(2)试判断线段
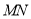 的长度是否随点
的长度是否随点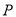 的位置的变化而改变?并说明理由.
的位置的变化而改变?并说明理由.(3)当
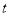 为何值时,四边形
为何值时,四边形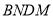 的面积最小.
的面积最小.(4)在
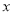 轴正半轴上存在点
轴正半轴上存在点 ,使得
,使得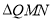 是等腰三角形,请直接写出不少于4个符合条件的点
是等腰三角形,请直接写出不少于4个符合条件的点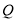 的坐标(用含
的坐标(用含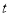 的式子表示)
的式子表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产的某种时令商品每件成本为
 元,经过市场调研发现,这种商品在未来
元,经过市场调研发现,这种商品在未来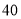 天内的日销售量
天内的日销售量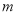 (件)与时间
(件)与时间 (天)的关系如下表所示.
(天)的关系如下表所示.时间
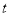 /天
/天1
3
6
10
36
……
日销售量
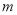 /件
/件94
90
84
76
24
……
未来40天内,前20天每天的价格
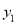 (元/件)与时间
(元/件)与时间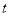 (天)的函数关系式为
(天)的函数关系式为 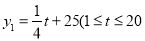 ,且
,且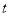 为整数),后20天每天的价格
为整数),后20天每天的价格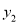 (元/件)与时间
(元/件)与时间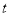 (天)的函数关系式为
(天)的函数关系式为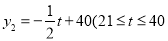 ,且
,且 为整数).
为整数).(Ⅰ)认真分析表格中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据
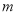 (件)与
(件)与 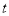 (天)的关系式;
(天)的关系式;(Ⅱ)试预测未来 40 天中哪一天的日销售利润最大,最大利润是多少?
(Ⅲ)在实际销售的前 20 天中,该公司决定每销售 1 件商品就捐赠
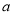 元利润
元利润 给希望工程. 公司通过销售记录发现,前 20 天中,每天扣除捐赠后的日销售利润随时间
给希望工程. 公司通过销售记录发现,前 20 天中,每天扣除捐赠后的日销售利润随时间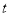 (天)的增大而增大,求
(天)的增大而增大,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
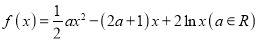 .
.(1)若曲线
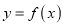 在
在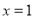 和
和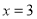 处的切线互相平行,求
处的切线互相平行,求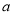 的值;
的值;(2)求
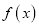 的单调区间;
的单调区间;(3)设
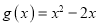 ,若对任意
,若对任意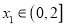 ,均存在
,均存在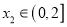 ,使得
,使得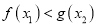 ,求
,求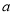 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有一个以
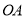 、
、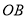 为半径的扇形池塘,在
为半径的扇形池塘,在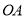 、
、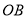 上分别取点
上分别取点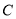 、
、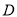 ,作
,作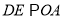 、
、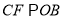 分别交弧
分别交弧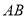 于点
于点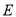 、
、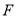 ,且
,且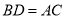 ,现用渔网沿着
,现用渔网沿着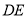 、
、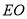 、
、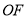 、
、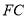 将池塘分成如图所示的养殖区域.已知
将池塘分成如图所示的养殖区域.已知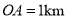 ,
, 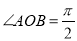 ,
, 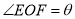 (
(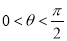 ).
).(1)若区域Ⅱ的总面积为
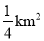 ,求
,求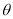 的值;
的值;(2)若养殖区域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分别是30万元、40万元、20万元,试问:当
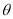 为多少时,年总收入最大?
为多少时,年总收入最大?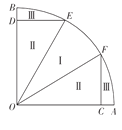
相关试题

