【题目】某高职院校进行自主招生文化素质考试,考试内容为语文、数学、英语三科,总分为200分.现从上线的考生中随机抽取20人,将其成绩用茎叶图记录如下:
男 | 女 | |||||||||||
15 | 6 | |||||||||||
5 | 4 | 16 | 3 | 5 | 8 | |||||||
8 | 2 | 17 | 2 | 3 | 6 | 8 | 8 | 8 | ||||
6 | 5 | 18 | 5 | 7 | ||||||||
19 | 2 | 3 | ||||||||||
(Ⅰ)计算上线考生中抽取的男生成绩的方差![]() ;(结果精确到小数点后一位)
;(结果精确到小数点后一位)
(Ⅱ)从上述茎叶图180分以上的考生中任选2人作为考生代表出席座谈会,求所选考生恰为一男一女的概率.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:根据茎叶图中提供的数据,可以求出统计量,如众数、中位数、均值、方差等,要记住公式,计算要准确.求概率问题,列出基本事件的种数时一定要根据题意去列,有的题用列表法,有的题只能列举,列举时要按规律去列,以保证不重不漏.
试题解析:(Ⅰ)依题意:样本中男生共6人,成绩分别为164、165、172、178、185、186.
![]() 他们的总分为1050,平均分为175.
他们的总分为1050,平均分为175.
![]()
![]()
![]() .
.
(Ⅱ)样本中180分以上的考生有男生2人,记为![]() 、
、![]() ,女生4人,记为
,女生4人,记为![]() 、
、![]() 、
、![]() 、
、![]() ,
,
从中任选2人,有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共15种,
共15种,
符合条件的有: ![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 8种,
8种,
故所求概率![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
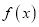 是R上的偶函数,且当x>0时,函数的解析式为
是R上的偶函数,且当x>0时,函数的解析式为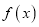 =
=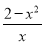 .
.(1)判断并证明
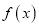 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;(2)求:当x<0时,函数
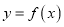 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
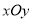 中,直线
中,直线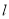 的参数方程是
的参数方程是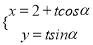 (
(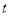 为参数),以
为参数),以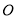 为极点,
为极点, 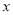 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线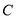 的极坐标方程为
的极坐标方程为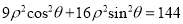 ,且直线
,且直线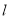 与曲线
与曲线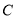 交于
交于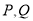 两点.
两点.(Ⅰ)求曲线
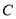 的直角坐标方程及直线
的直角坐标方程及直线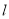 恒过的定点
恒过的定点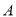 的坐标;
的坐标;(Ⅱ)在(Ⅰ)的条件下,若
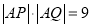 ,求直线
,求直线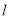 的普通方程.
的普通方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
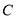 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在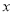 轴上,焦点到短轴端点的距离为2,离心率为
轴上,焦点到短轴端点的距离为2,离心率为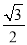 .
.(Ⅰ)求该椭圆的方程;
(Ⅱ)若直线
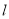 与椭圆
与椭圆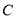 交于
交于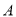 ,
, 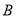 两点且
两点且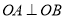 ,是否存在以原点
,是否存在以原点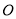 为圆心的定圆与直线
为圆心的定圆与直线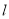 相切?若存在求出定圆的方程;若不存在,请说明理由
相切?若存在求出定圆的方程;若不存在,请说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. “
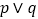 为真”是“
为真”是“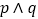 为真”的充分不必要条件;
为真”的充分不必要条件;B. 样本
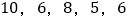 的标准差是3.3;
的标准差是3.3;C. K2是用来判断两个分类变量是否相关的随机变量,当K2的值很小时可以推定两类变量不相关;
D. 设有一个回归直线方程为
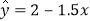 ,则变量
,则变量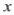 每增加一个单位,
每增加一个单位,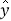 平均减少1.5个单位.
平均减少1.5个单位. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知奇函数
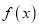 在区间
在区间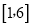 上是增函数,且最大值为10,最小值为4,则在区间
上是增函数,且最大值为10,最小值为4,则在区间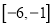 上
上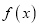 的最大值、最小值分别是( )
的最大值、最小值分别是( )A. -4,-10 B. 4,-10
C. 10,4 D. 不确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
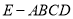 中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.(1)求
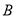 到平面
到平面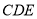 的距离
的距离(2)在线段
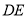 上是否存在一点
上是否存在一点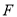 ,使
,使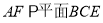 ?若存在,求出
?若存在,求出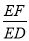 的值;若不存在,说明理由.
的值;若不存在,说明理由.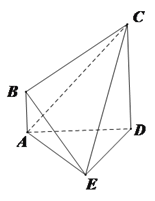
相关试题

