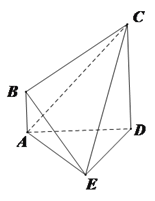
【题目】如图,在四棱锥![]() 中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(1)求![]() 到平面
到平面![]() 的距离
的距离
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
参考答案:
【答案】(I)![]() (II)见解析.
(II)见解析.
【解析】试题分析:
(1)利用等体积法结合题意可求得![]() 到平面
到平面![]() 的距离为
的距离为![]() ;
;
(2)当![]() 时满足题意,利用题中所给的条件进行证明即可.
时满足题意,利用题中所给的条件进行证明即可.
试题解析:
解:(1)方法一:因为![]() 平面
平面![]() ,
, ![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() ,所以
,所以![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
方法二:等积法求高.
(2)解:在线段![]() 上存在一点
上存在一点![]() ,使
,使![]() 平面
平面![]() ,
,
下面给出证明:设![]() 为线段
为线段![]() 上的一点,且
上的一点,且![]() ,
,
过点![]() 作
作![]() 交于点
交于点![]() ,则
,则![]() ,
,
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() ,
,
所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,又
,又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高职院校进行自主招生文化素质考试,考试内容为语文、数学、英语三科,总分为200分.现从上线的考生中随机抽取20人,将其成绩用茎叶图记录如下:
男
女
15
6
5
4
16
3
5
8
8
2
17
2
3
6
8
8
8
6
5
18
5
7
19
2
3
(Ⅰ)计算上线考生中抽取的男生成绩的方差
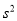 ;(结果精确到小数点后一位)
;(结果精确到小数点后一位)(Ⅱ)从上述茎叶图180分以上的考生中任选2人作为考生代表出席座谈会,求所选考生恰为一男一女的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. “
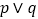 为真”是“
为真”是“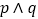 为真”的充分不必要条件;
为真”的充分不必要条件;B. 样本
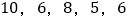 的标准差是3.3;
的标准差是3.3;C. K2是用来判断两个分类变量是否相关的随机变量,当K2的值很小时可以推定两类变量不相关;
D. 设有一个回归直线方程为
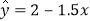 ,则变量
,则变量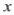 每增加一个单位,
每增加一个单位,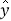 平均减少1.5个单位.
平均减少1.5个单位. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知奇函数
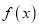 在区间
在区间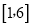 上是增函数,且最大值为10,最小值为4,则在区间
上是增函数,且最大值为10,最小值为4,则在区间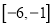 上
上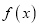 的最大值、最小值分别是( )
的最大值、最小值分别是( )A. -4,-10 B. 4,-10
C. 10,4 D. 不确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知坐标平面上点
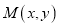 与两个定点
与两个定点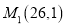 ,
, 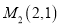 的距离之比等于5.
的距离之比等于5.(1)求点
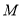 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;(2)记(1)中的轨迹为
 ,过点
,过点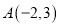 的直线
的直线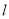 被
被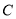 所截得的线段的长为 8,求直线
所截得的线段的长为 8,求直线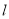 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=xlnx,g(x)=x3+ax2-x+2.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)对任意x∈(0,+∞),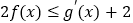 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
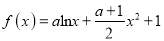 .
.(1)当
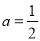 时,求
时,求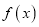 在区间
在区间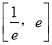 上的最值;
上的最值;(2)讨论函数
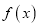 的单调性;
的单调性;(3)当
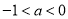 时,有
时,有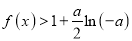 恒成立,求
恒成立,求 的取值范围.
的取值范围.
相关试题

