【题目】已知函数![]() 是R上的偶函数,且当x>0时,函数的解析式为
是R上的偶函数,且当x>0时,函数的解析式为![]() =
=![]() .
.
(1)判断并证明![]() 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;
(2)求:当x<0时,函数![]() 的解析式.
的解析式.
参考答案:
【答案】(1)详见解析;(2) ![]() .
.
【解析】试题分析:用定义证明函数的单调性需要以下步骤,一、取值,在x>0内任取两个自变量![]() ,且
,且![]() ,二、作差
,二、作差![]() ,三、变形(包括通分、配方、因式分解、分子有理化等),四、断号(判断各部分的正负,说明差的符号正负),最后给出结论.利用函数的奇偶性求函数的解析式是函数的奇偶性的应用之一,给出函数在x>0的解析式,利用当x<0时,-x>0,借助f(x)=f(-x)就可以求出x<0时的解析式;
,三、变形(包括通分、配方、因式分解、分子有理化等),四、断号(判断各部分的正负,说明差的符号正负),最后给出结论.利用函数的奇偶性求函数的解析式是函数的奇偶性的应用之一,给出函数在x>0的解析式,利用当x<0时,-x>0,借助f(x)=f(-x)就可以求出x<0时的解析式;
试题解析:
(1)当![]() 时,
时, ![]()
![]()
![]() 是
是![]() 上减函数
上减函数
证明: ![]() 且
且![]()
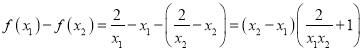
![]()
![]()
![]() 即
即![]()
![]() 是
是![]() 上减函数.
上减函数.
当![]() 时,
时, ![]()
![]() 为R上偶函数
为R上偶函数![]()
![]() 当
当![]() 时,
时, ![]() .
.
【点精】函数的单调性的判断分为“粗判”和“细断”两种,所谓粗判,就是根据已知函数的单调性结合和复合函数关系,判断出函数在某区间上的单调性;所谓细断就是根据函数的单调性定义进行严格证明或利用导数的正负进行严格的判断,关于利用函数的单调性的定义证明,其步骤为①取值,②作差,③变形,④断号,最后给出单调性结论. 利用函数的奇偶性求函数的解析式是函数的奇偶性的应用之一,给出函数在x>0的解析式,利用当xlt;0时,-x>0,偶函数借助f(x)=f(-x)就可以求出x<0时的解析式;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
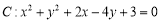 .
.(1)若不经过坐标原点的直线
 与圆
与圆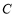 相切,且直线
相切,且直线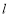 在两坐标轴上的截距相等,求直线
在两坐标轴上的截距相等,求直线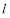 的方程;
的方程;(2)设点
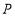 在圆
在圆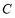 上,求点
上,求点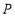 到直线
到直线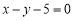 距离的最大值与最小值.
距离的最大值与最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们可以用随机模拟的方法估计
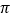 的值,如图程序框图表示其基本步骤(函数
的值,如图程序框图表示其基本步骤(函数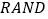 是产生随机数的函数,它能随机产生
是产生随机数的函数,它能随机产生 内的任何一个实数).若输出的结果为
内的任何一个实数).若输出的结果为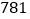 ,则由此可估计
,则由此可估计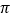 的近似值为( )
的近似值为( )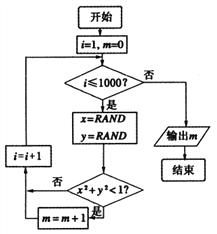
A. 3.119 B. 3.124 C. 3.132 D. 3.151
-
科目: 来源: 题型:
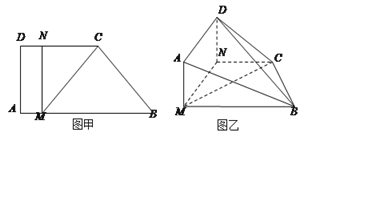
查看答案和解析>>【题目】如图甲,直角梯形
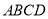 中,
中, 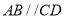 ,
, 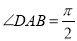 ,点
,点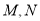 分别在
分别在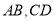 上,且
上,且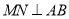 ,
, 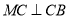 ,
, 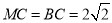 ,现将梯形
,现将梯形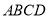 沿
沿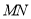 折起,使平面
折起,使平面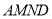 与平面
与平面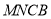 垂直(如图乙).
垂直(如图乙).(Ⅰ)求证:
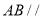 平面
平面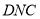 ;
;
(II)当
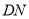 的长为何值时,二面角
的长为何值时,二面角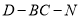 的大小为
的大小为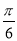 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
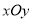 中,直线
中,直线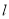 的参数方程是
的参数方程是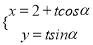 (
(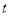 为参数),以
为参数),以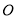 为极点,
为极点, 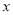 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线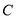 的极坐标方程为
的极坐标方程为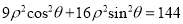 ,且直线
,且直线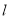 与曲线
与曲线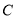 交于
交于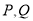 两点.
两点.(Ⅰ)求曲线
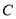 的直角坐标方程及直线
的直角坐标方程及直线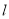 恒过的定点
恒过的定点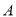 的坐标;
的坐标;(Ⅱ)在(Ⅰ)的条件下,若
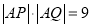 ,求直线
,求直线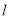 的普通方程.
的普通方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
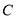 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在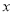 轴上,焦点到短轴端点的距离为2,离心率为
轴上,焦点到短轴端点的距离为2,离心率为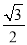 .
.(Ⅰ)求该椭圆的方程;
(Ⅱ)若直线
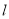 与椭圆
与椭圆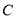 交于
交于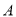 ,
, 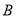 两点且
两点且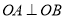 ,是否存在以原点
,是否存在以原点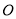 为圆心的定圆与直线
为圆心的定圆与直线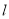 相切?若存在求出定圆的方程;若不存在,请说明理由
相切?若存在求出定圆的方程;若不存在,请说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】某高职院校进行自主招生文化素质考试,考试内容为语文、数学、英语三科,总分为200分.现从上线的考生中随机抽取20人,将其成绩用茎叶图记录如下:
男
女
15
6
5
4
16
3
5
8
8
2
17
2
3
6
8
8
8
6
5
18
5
7
19
2
3
(Ⅰ)计算上线考生中抽取的男生成绩的方差
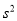 ;(结果精确到小数点后一位)
;(结果精确到小数点后一位)(Ⅱ)从上述茎叶图180分以上的考生中任选2人作为考生代表出席座谈会,求所选考生恰为一男一女的概率.
相关试题

