【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(Ⅰ)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 恒过的定点
恒过的定点![]() 的坐标;
的坐标;
(Ⅱ)在(Ⅰ)的条件下,若![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
参考答案:
【答案】(Ⅰ)![]() :
:![]() ,
,![]() ; (Ⅱ)
; (Ⅱ)![]() .
.
【解析】试题分析:(1)利用三种方程的转化方法,求出普通方程,即可求曲线C的普通方程及直线l恒过的定点A的坐标;
(2)在(1)的条件下,若![]() ,利用参数的几何意义,求出
,利用参数的几何意义,求出![]() ,即可求直线L的普通方程.
,即可求直线L的普通方程.
试题解析:
(Ⅰ)因为x=ρcosθ,y=ρsinθ,所以C: ![]() ,直线l恒过定点为
,直线l恒过定点为![]() .
.
(Ⅱ)把直线l的方程代入曲线C的直角坐标方程中得: ![]() .
.
由t的几何意义知![]() ,
, ![]() ,因为点A在椭圆内,这个方程必有两个实根,
,因为点A在椭圆内,这个方程必有两个实根,
所以![]() ,因为
,因为![]() ,即
,即![]() ,
,
所以![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
因此,直线l的方程为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们可以用随机模拟的方法估计
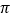 的值,如图程序框图表示其基本步骤(函数
的值,如图程序框图表示其基本步骤(函数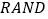 是产生随机数的函数,它能随机产生
是产生随机数的函数,它能随机产生 内的任何一个实数).若输出的结果为
内的任何一个实数).若输出的结果为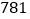 ,则由此可估计
,则由此可估计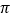 的近似值为( )
的近似值为( )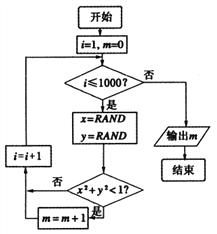
A. 3.119 B. 3.124 C. 3.132 D. 3.151
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,直角梯形
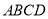 中,
中, 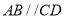 ,
, 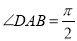 ,点
,点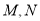 分别在
分别在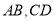 上,且
上,且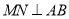 ,
, 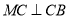 ,
, 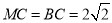 ,现将梯形
,现将梯形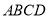 沿
沿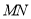 折起,使平面
折起,使平面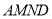 与平面
与平面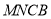 垂直(如图乙).
垂直(如图乙).(Ⅰ)求证:
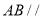 平面
平面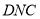 ;
;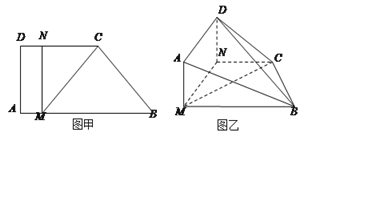
(II)当
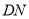 的长为何值时,二面角
的长为何值时,二面角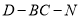 的大小为
的大小为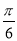 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
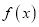 是R上的偶函数,且当x>0时,函数的解析式为
是R上的偶函数,且当x>0时,函数的解析式为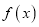 =
=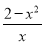 .
.(1)判断并证明
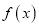 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;(2)求:当x<0时,函数
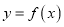 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
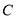 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在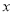 轴上,焦点到短轴端点的距离为2,离心率为
轴上,焦点到短轴端点的距离为2,离心率为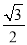 .
.(Ⅰ)求该椭圆的方程;
(Ⅱ)若直线
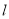 与椭圆
与椭圆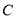 交于
交于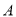 ,
, 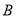 两点且
两点且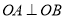 ,是否存在以原点
,是否存在以原点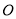 为圆心的定圆与直线
为圆心的定圆与直线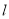 相切?若存在求出定圆的方程;若不存在,请说明理由
相切?若存在求出定圆的方程;若不存在,请说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】某高职院校进行自主招生文化素质考试,考试内容为语文、数学、英语三科,总分为200分.现从上线的考生中随机抽取20人,将其成绩用茎叶图记录如下:
男
女
15
6
5
4
16
3
5
8
8
2
17
2
3
6
8
8
8
6
5
18
5
7
19
2
3
(Ⅰ)计算上线考生中抽取的男生成绩的方差
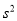 ;(结果精确到小数点后一位)
;(结果精确到小数点后一位)(Ⅱ)从上述茎叶图180分以上的考生中任选2人作为考生代表出席座谈会,求所选考生恰为一男一女的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. “
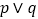 为真”是“
为真”是“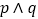 为真”的充分不必要条件;
为真”的充分不必要条件;B. 样本
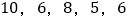 的标准差是3.3;
的标准差是3.3;C. K2是用来判断两个分类变量是否相关的随机变量,当K2的值很小时可以推定两类变量不相关;
D. 设有一个回归直线方程为
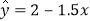 ,则变量
,则变量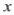 每增加一个单位,
每增加一个单位,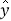 平均减少1.5个单位.
平均减少1.5个单位.
相关试题

