【题目】如图,F1,F2分别是椭圆C:![]() 的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
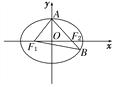
(1)求椭圆C的离心率;
(2)已知△AF1B的面积为40![]() ,求a,b的值.
,求a,b的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】(1)由题意可知,△AF1F2为等边三角形,a=2c,所以e=![]() .
.
(2)方法一:a2=4c2,b2=3c2,直线AB的方程为y=-![]() (x-c),
(x-c),
将其代入椭圆方程3x2+4y2=12c2,得B![]() ,
,
所以|AB|=![]() ..
..
由S△AF1B=![]() |AF1|·|AB|·sin∠F1AB=
|AF1|·|AB|·sin∠F1AB=![]() a·
a·![]() c·
c·![]() =
=![]() a2=40
a2=40![]() ,
,
解得a=10,b=5![]() .
.
方法二:设|AB|=t.因为|AF2|=a,所以|BF2|=t-a,
由椭圆定义|BF1|+|BF2|=2a可知,|BF1|=3a-t,
再由余弦定理(3a-t)2=a2+t2-2atcos 60°可得,t=![]() a,
a,
由S△AF1B=![]() a
a![]() a
a![]() =
=![]() a2=40
a2=40![]() 知,a=10,b=5
知,a=10,b=5![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2的正方形ABCD的顶点A,D,分别在x轴,y轴正半轴上移动,则

 的最大值为 .
的最大值为 . 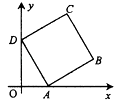
-
科目: 来源: 题型:
查看答案和解析>>【题目】设两个非零向量
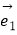 和
和  不共线.
不共线.
(1)如果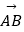 =
= 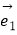 +
+  ,
, 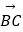 =2
=2 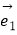 +8
+8  ,
, 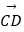 =3
=3 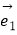 ﹣3
﹣3  ,求证:A、B、D三点共线;
,求证:A、B、D三点共线;
(2)若|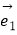 |=2,|
|=2,|  |=3,
|=3, 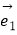 与
与  的夹角为60°,是否存在实数m,使得m
的夹角为60°,是否存在实数m,使得m 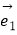 +
+  与
与 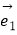 ﹣
﹣  垂直?并说明理由.
垂直?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】从“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中,选出适当的一种填空:
(1)记集合A={-1,p,2},B={2,3},则“p=3”是“A∩B=B”的__________________;
(2)“a=1”是“函数f(x)=|2x-a|在区间
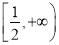 上为增函数”的________________.
上为增函数”的________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
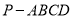 中,四边形
中,四边形 是直角梯形,
是直角梯形,  ,
,  ,
,  底面
底面 ,
,  ,
,  ,
,  是
是 的中点.
的中点.
(1)求证:平面
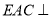 平面
平面 ;
;(2)若二面角
 的余弦值为
的余弦值为 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=4cosxsin(x+
 )﹣1.
)﹣1.
(1)求f(x)的最小正周期;
(2)若函数f(x)的定义域为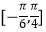 ,求单调递减区间和值域.
,求单调递减区间和值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在坐标原点、焦点在x轴上的椭圆,它的离心率为
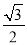 ,且与直线x+y-1=0相交于M、N两点,若以MN为直径的圆经过坐标原点,求椭圆的方程.
,且与直线x+y-1=0相交于M、N两点,若以MN为直径的圆经过坐标原点,求椭圆的方程.
相关试题

